Сообщение Re[23]: О несимметричных процессах (что мешает обратить врем от 13.07.2018 12:54
Изменено 13.07.2018 12:59 D. Mon
Re[23]: О несимметричных процессах (что мешает обратить врем
Здравствуйте, vdimas, Вы писали:
V>>>Прямо на горизонте событий эта вторая космическая в точности равна скорости света.
DM>>Да. И если бы она была актуальна, то по определению второй космической свет мог бы улететь с горизонта на бесконечноть.
V>Каким образом?
V>На второй космической свет будет вечно бегать по горизонту.
V>Чтобы убежать с горизонта, эту скорость надо преодолеть.
Еще раз. Рассматриваем (для простоты) исключительно вертикальное движение, никаких орбит.
Ньютоновская гравитация.
Если материальная точка свободно падает с бесконечности на нашу идеальную планету, то на радиусе R она будет иметь такую-то скорость v.
Это можно прокрутить в обратном направлении: если на радиусе R наша материальная точка имеет вертикальную скорость v, она улетит на бесконечность. То же самое уравнение, просто время обратили.
Подставляем v=c, получаем радиус 2GM/c^2.
Теперь берем ОТО. Берем свет, который должен иметь скорость с, пускаем его вертикально вверх с радиуса 2GM/c^2. По определению выше, он должен улететь на бесконечность. А по логике и уравнениям ОТО — не улетит.
V>В этом-то и прикол — "вертикальная" и "касательная" вторые космические скорости у поверхности массивного объекта в точности равны.
V>Т.е. направление не важно.
Обоснуй.
DM>>И не "внутри которого", а "включая который", это важная разница.
V>Боюсь, эта разница описывается понятием математического предела.
Нет, предел тут не при чем.
V>Т.е., ты решил поспорить о величинах, отличающихся друг от друга сколь угодно мало.
Там качественная разница в траекториях, я лишь показываю простейший пример.
Давай пока не будем отвлекаться на РТГ, на решения Керра, квазары и прочий оффтоп. Сначала с ОТО и Шварцшильдом разберемся.
V>Далее.
V>Сила тяжести на горизонте и даже за ним НЕ является бесконечной величиной, а вполне конечна и вычисляема.
V>Например, ЧД Стрелец А, масса ~4.3*106 солнечных или 8.6*1036 кг.
V>Радиус Г.С.:R=2MG/c2
V>Ускорение свободного падения на Г.С.:g=MG/R2
Как ты получил этот результат? По формулам ньютоновской гравитации? Это неправильно, они неприменимы для ЧД.
В ОТО есть понятие поверхностной гравитации. Для решения Шварцшильда на горизонте это что-то вроде c^2 / 4GM.
V>Например, мы находимся на 1 тыс км над горизонтом этой ЧД, пусть наш волшебный трос будет 2 тыс км, т.е. датчик нырнул за горизонт на 1 тыс км.
V>С точностью до 3-го порядка вес тела на такой "глубине" при упомянутой скорости вращения будет всего в ~28.3 раза больше земного. Это более чем конечные числа.
V>Что помешает вытянуть такой датчик обратно? ))
Геометрия пространства-времени помешает. Ты с ОТО совсем-совсем не знаком?
DM>>Во-вторых, в ОТО в метрике Шварцшильда двигаться по круговой орбите со скоростью света получится только на радиусе 1.5R, т.е. отнюдь не на горизонте, а в полтора раза дальше.
V>Ты, наверно, имеешь ввиду первую космическую?
V>Тогда не 1.5R, а sqrt(2)R, т.е. ~1.42*R.
Нет, я имею в виду решения ОТО про геодезические для света. См. https://en.wikipedia.org/wiki/Photon_sphere
Не надо ньютоновские формулы для ЧД продолжать использовать, это фейспалм.
DM>>Это популярная ошибка — объяснять горизонт второй космической.
V>А можно несколько ссылок на развенчание этой "ошибки", если она такая популярная?
Постараюсь найти что-то конкретное, а то пока хочется просто послать к любому учебнику по ОТО.
DM>>Там совсем другой механизм. Там другое притяжение: ньютоновская гравитация и ОТО отличаются численно вблизи массивных тел, там формула гравитационного потенциала разная, в ОТО гравитация "сильнее".
V>При чём тут вообще ньютоновская гравитация?
V>Давай оставаться в рамках ОТО.
Вот именно, давай.
V>Насчёт в "ОТО гравитация сильнее" — это зависит от массы ЧД, вернее, от радиуса её горизонта событий.
Числа зависят да, но важно, что есть качественная разница: реально отличаются формулы и траектории. Ты не получишь правильные траектории для движения света и материальных тел вблизи ЧД и просто массивных звезд, пользуясь ньютоновскими формулами.

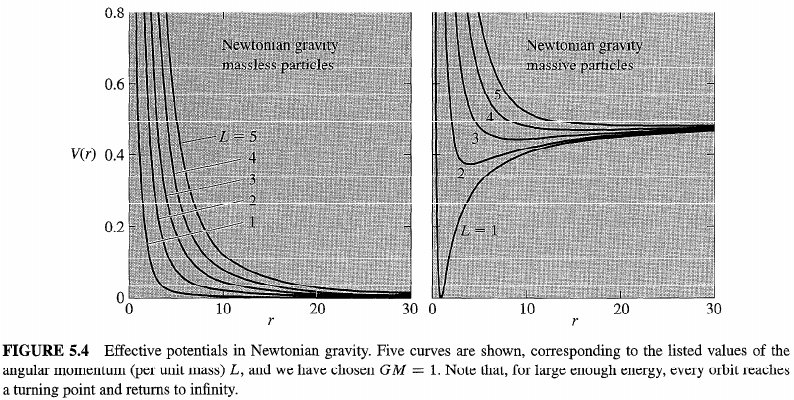
см. https://en.wikipedia.org/wiki/Schwarzschild_geodesics
V>Ну и, релятивистское увеличение массы не сказывается на ускорении свободного падения.
Это здесь вообще не при чем.
DM>>Или бросить камень с горизонта вверх, он бы подлетел на некоторую высоту над горизонтом и упал бы обратно. Как это работает в ньютоновской гравитации. Но в ОТО это работает иначе, там камень не взлетит с горионта ни на сколько, и даже свет не взлетит.
V>Верно, бо вторая космическая там равна скорости света.
V>Причём, во всех абсолютно направлениях.
V>(с точностью до описани происходящего в случае эллиптического движения)
Подожди пока с направлениями. Тут принципиальный момент: можно ли с горизонта подбросить камень хоть на метр? В ньютоновской механике — можно. В ОТО — нельзя. Ты пока никак не увидишь разницу, похоже, а она важная.
DM>>Камень будет всегда падать вниз, а свет или упадет, или в лучшем случае (будучи пущен строго вверх) останется на горизонте.
V>Строго по касательной если — тоже останется на горизонте (предположим, мы говорим о пределе справа, т.е. сколь угодно близки к горизонту снаружи).
Нет, свет, пущенный ниже фотонной сферы горизонтально, не будет крутиться по орбите и не будет оставаться на горизонте. Он упадет в ЧД.
Тут надо хоть один учебник по ОТО открыть. Мне сложно дать более конкретную ссылку сейчас, чтобы было доходчиво.
V>>>Прямо на горизонте событий эта вторая космическая в точности равна скорости света.
DM>>Да. И если бы она была актуальна, то по определению второй космической свет мог бы улететь с горизонта на бесконечноть.
V>Каким образом?
V>На второй космической свет будет вечно бегать по горизонту.
V>Чтобы убежать с горизонта, эту скорость надо преодолеть.
Еще раз. Рассматриваем (для простоты) исключительно вертикальное движение, никаких орбит.
Ньютоновская гравитация.
Если материальная точка свободно падает с бесконечности на нашу идеальную планету, то на радиусе R она будет иметь такую-то скорость v.
Это можно прокрутить в обратном направлении: если на радиусе R наша материальная точка имеет вертикальную скорость v, она улетит на бесконечность. То же самое уравнение, просто время обратили.
Подставляем v=c, получаем радиус 2GM/c^2.
Теперь берем ОТО. Берем свет, который должен иметь скорость с, пускаем его вертикально вверх с радиуса 2GM/c^2. По определению выше, он должен улететь на бесконечность. А по логике и уравнениям ОТО — не улетит.
V>В этом-то и прикол — "вертикальная" и "касательная" вторые космические скорости у поверхности массивного объекта в точности равны.
V>Т.е. направление не важно.
Обоснуй.
DM>>И не "внутри которого", а "включая который", это важная разница.
V>Боюсь, эта разница описывается понятием математического предела.
Нет, предел тут не при чем.
V>Т.е., ты решил поспорить о величинах, отличающихся друг от друга сколь угодно мало.
Там качественная разница в траекториях, я лишь показываю простейший пример.
Давай пока не будем отвлекаться на РТГ, на решения Керра, квазары и прочий оффтоп. Сначала с ОТО и Шварцшильдом разберемся.
V>Далее.
V>Сила тяжести на горизонте и даже за ним НЕ является бесконечной величиной, а вполне конечна и вычисляема.
V>Например, ЧД Стрелец А, масса ~4.3*106 солнечных или 8.6*1036 кг.
V>Радиус Г.С.:R=2MG/c2
V>Ускорение свободного падения на Г.С.:g=MG/R2
Как ты получил этот результат? По формулам ньютоновской гравитации? Это неправильно, они неприменимы для ЧД.
В ОТО есть понятие поверхностной гравитации. Для решения Шварцшильда на горизонте это что-то вроде c^2 / 4GM.
V>Например, мы находимся на 1 тыс км над горизонтом этой ЧД, пусть наш волшебный трос будет 2 тыс км, т.е. датчик нырнул за горизонт на 1 тыс км.
V>С точностью до 3-го порядка вес тела на такой "глубине" при упомянутой скорости вращения будет всего в ~28.3 раза больше земного. Это более чем конечные числа.
V>Что помешает вытянуть такой датчик обратно? ))
Геометрия пространства-времени помешает. Ты с ОТО совсем-совсем не знаком?
DM>>Во-вторых, в ОТО в метрике Шварцшильда двигаться по круговой орбите со скоростью света получится только на радиусе 1.5R, т.е. отнюдь не на горизонте, а в полтора раза дальше.
V>Ты, наверно, имеешь ввиду первую космическую?
V>Тогда не 1.5R, а sqrt(2)R, т.е. ~1.42*R.
Нет, я имею в виду решения ОТО про геодезические для света. См. https://en.wikipedia.org/wiki/Photon_sphere
Не надо ньютоновские формулы для ЧД продолжать использовать, это фейспалм.
DM>>Это популярная ошибка — объяснять горизонт второй космической.
V>А можно несколько ссылок на развенчание этой "ошибки", если она такая популярная?
Постараюсь найти что-то конкретное, а то пока хочется просто послать к любому учебнику по ОТО.
DM>>Там совсем другой механизм. Там другое притяжение: ньютоновская гравитация и ОТО отличаются численно вблизи массивных тел, там формула гравитационного потенциала разная, в ОТО гравитация "сильнее".
V>При чём тут вообще ньютоновская гравитация?
V>Давай оставаться в рамках ОТО.
Вот именно, давай.
V>Насчёт в "ОТО гравитация сильнее" — это зависит от массы ЧД, вернее, от радиуса её горизонта событий.
Числа зависят да, но важно, что есть качественная разница: реально отличаются формулы и траектории. Ты не получишь правильные траектории для движения света и материальных тел вблизи ЧД и просто массивных звезд, пользуясь ньютоновскими формулами.


см. https://en.wikipedia.org/wiki/Schwarzschild_geodesics
V>Ну и, релятивистское увеличение массы не сказывается на ускорении свободного падения.
Это здесь вообще не при чем.
DM>>Или бросить камень с горизонта вверх, он бы подлетел на некоторую высоту над горизонтом и упал бы обратно. Как это работает в ньютоновской гравитации. Но в ОТО это работает иначе, там камень не взлетит с горионта ни на сколько, и даже свет не взлетит.
V>Верно, бо вторая космическая там равна скорости света.
V>Причём, во всех абсолютно направлениях.
V>(с точностью до описани происходящего в случае эллиптического движения)
Подожди пока с направлениями. Тут принципиальный момент: можно ли с горизонта подбросить камень хоть на метр? В ньютоновской механике — можно. В ОТО — нельзя. Ты пока никак не увидишь разницу, похоже, а она важная.
DM>>Камень будет всегда падать вниз, а свет или упадет, или в лучшем случае (будучи пущен строго вверх) останется на горизонте.
V>Строго по касательной если — тоже останется на горизонте (предположим, мы говорим о пределе справа, т.е. сколь угодно близки к горизонту снаружи).
Нет, свет, пущенный ниже фотонной сферы горизонтально, не будет крутиться по орбите и не будет оставаться на горизонте. Он упадет в ЧД.
Тут надо хоть один учебник по ОТО открыть. Мне сложно дать более конкретную ссылку сейчас, чтобы было доходчиво.
Re[23]: О несимметричных процессах (что мешает обратить врем
Здравствуйте, vdimas, Вы писали:
V>>>Прямо на горизонте событий эта вторая космическая в точности равна скорости света.
DM>>Да. И если бы она была актуальна, то по определению второй космической свет мог бы улететь с горизонта на бесконечноть.
V>Каким образом?
V>На второй космической свет будет вечно бегать по горизонту.
V>Чтобы убежать с горизонта, эту скорость надо преодолеть.
Еще раз. Рассматриваем (для простоты) исключительно вертикальное движение, никаких орбит.
Ньютоновская гравитация.
Если материальная точка свободно падает с бесконечности на нашу идеальную планету, то на радиусе R она будет иметь такую-то скорость v.
Это можно прокрутить в обратном направлении: если на радиусе R наша материальная точка имеет вертикальную скорость v, она улетит на бесконечность. То же самое уравнение, просто время обратили.
Подставляем v=c, получаем радиус 2GM/c^2.
Теперь берем ОТО. Берем свет, который должен иметь скорость с, пускаем его вертикально вверх с радиуса 2GM/c^2. По определению выше, он должен улететь на бесконечность. А по логике и уравнениям ОТО — не улетит.
V>В этом-то и прикол — "вертикальная" и "касательная" вторые космические скорости у поверхности массивного объекта в точности равны.
V>Т.е. направление не важно.
Обоснуй.
DM>>И не "внутри которого", а "включая который", это важная разница.
V>Боюсь, эта разница описывается понятием математического предела.
Нет, предел тут не при чем.
V>Т.е., ты решил поспорить о величинах, отличающихся друг от друга сколь угодно мало.
Там качественная разница в траекториях, я лишь показываю простейший пример.
Давай пока не будем отвлекаться на РТГ, на решения Керра, квазары и прочий оффтоп. Сначала с ОТО и Шварцшильдом разберемся.
V>Далее.
V>Сила тяжести на горизонте и даже за ним НЕ является бесконечной величиной, а вполне конечна и вычисляема.
V>Например, ЧД Стрелец А, масса ~4.3*106 солнечных или 8.6*1036 кг.
V>Радиус Г.С.:R=2MG/c2
V>Ускорение свободного падения на Г.С.:g=MG/R2
Как ты получил этот результат? По формулам ньютоновской гравитации? Это неправильно, они неприменимы для ЧД.
В ОТО есть понятие поверхностной гравитации. Для решения Шварцшильда на горизонте это что-то вроде c^2 / 4GM.
V>Например, мы находимся на 1 тыс км над горизонтом этой ЧД, пусть наш волшебный трос будет 2 тыс км, т.е. датчик нырнул за горизонт на 1 тыс км.
V>С точностью до 3-го порядка вес тела на такой "глубине" при упомянутой скорости вращения будет всего в ~28.3 раза больше земного. Это более чем конечные числа.
V>Что помешает вытянуть такой датчик обратно? ))
Геометрия пространства-времени помешает. Ты с ОТО совсем-совсем не знаком?
DM>>Во-вторых, в ОТО в метрике Шварцшильда двигаться по круговой орбите со скоростью света получится только на радиусе 1.5R, т.е. отнюдь не на горизонте, а в полтора раза дальше.
V>Ты, наверно, имеешь ввиду первую космическую?
V>Тогда не 1.5R, а sqrt(2)R, т.е. ~1.42*R.
Нет, я имею в виду решения ОТО про геодезические для света. См. https://en.wikipedia.org/wiki/Photon_sphere
Не надо ньютоновские формулы для ЧД продолжать использовать, это фейспалм.
DM>>Это популярная ошибка — объяснять горизонт второй космической.
V>А можно несколько ссылок на развенчание этой "ошибки", если она такая популярная?
Постараюсь найти что-то конкретное, а то пока хочется просто послать к любому учебнику по ОТО.
DM>>Там совсем другой механизм. Там другое притяжение: ньютоновская гравитация и ОТО отличаются численно вблизи массивных тел, там формула гравитационного потенциала разная, в ОТО гравитация "сильнее".
V>При чём тут вообще ньютоновская гравитация?
V>Давай оставаться в рамках ОТО.
Вот именно, давай.
V>Насчёт в "ОТО гравитация сильнее" — это зависит от массы ЧД, вернее, от радиуса её горизонта событий.
Числа зависят да, но важно, что есть качественная разница: реально отличаются формулы и траектории. Ты не получишь правильные траектории для движения света и материальных тел вблизи ЧД и просто массивных звезд, пользуясь ньютоновскими формулами.



см. https://en.wikipedia.org/wiki/Schwarzschild_geodesics
V>Ну и, релятивистское увеличение массы не сказывается на ускорении свободного падения.
Это здесь вообще не при чем.
DM>>Или бросить камень с горизонта вверх, он бы подлетел на некоторую высоту над горизонтом и упал бы обратно. Как это работает в ньютоновской гравитации. Но в ОТО это работает иначе, там камень не взлетит с горионта ни на сколько, и даже свет не взлетит.
V>Верно, бо вторая космическая там равна скорости света.
V>Причём, во всех абсолютно направлениях.
V>(с точностью до описани происходящего в случае эллиптического движения)
Подожди пока с направлениями. Тут принципиальный момент: можно ли с горизонта подбросить камень хоть на метр? В ньютоновской механике — можно. В ОТО — нельзя. Ты пока никак не увидишь разницу, похоже, а она важная.
DM>>Камень будет всегда падать вниз, а свет или упадет, или в лучшем случае (будучи пущен строго вверх) останется на горизонте.
V>Строго по касательной если — тоже останется на горизонте (предположим, мы говорим о пределе справа, т.е. сколь угодно близки к горизонту снаружи).
Нет, свет, пущенный ниже фотонной сферы горизонтально, не будет крутиться по орбите и не будет оставаться на горизонте. Он упадет в ЧД.
Тут надо хоть один учебник по ОТО открыть. Мне сложно дать более конкретную ссылку сейчас, чтобы было доходчиво.
V>>>Прямо на горизонте событий эта вторая космическая в точности равна скорости света.
DM>>Да. И если бы она была актуальна, то по определению второй космической свет мог бы улететь с горизонта на бесконечноть.
V>Каким образом?
V>На второй космической свет будет вечно бегать по горизонту.
V>Чтобы убежать с горизонта, эту скорость надо преодолеть.
Еще раз. Рассматриваем (для простоты) исключительно вертикальное движение, никаких орбит.
Ньютоновская гравитация.
Если материальная точка свободно падает с бесконечности на нашу идеальную планету, то на радиусе R она будет иметь такую-то скорость v.
Это можно прокрутить в обратном направлении: если на радиусе R наша материальная точка имеет вертикальную скорость v, она улетит на бесконечность. То же самое уравнение, просто время обратили.
Подставляем v=c, получаем радиус 2GM/c^2.
Теперь берем ОТО. Берем свет, который должен иметь скорость с, пускаем его вертикально вверх с радиуса 2GM/c^2. По определению выше, он должен улететь на бесконечность. А по логике и уравнениям ОТО — не улетит.
V>В этом-то и прикол — "вертикальная" и "касательная" вторые космические скорости у поверхности массивного объекта в точности равны.
V>Т.е. направление не важно.
Обоснуй.
DM>>И не "внутри которого", а "включая который", это важная разница.
V>Боюсь, эта разница описывается понятием математического предела.
Нет, предел тут не при чем.
V>Т.е., ты решил поспорить о величинах, отличающихся друг от друга сколь угодно мало.
Там качественная разница в траекториях, я лишь показываю простейший пример.
Давай пока не будем отвлекаться на РТГ, на решения Керра, квазары и прочий оффтоп. Сначала с ОТО и Шварцшильдом разберемся.
V>Далее.
V>Сила тяжести на горизонте и даже за ним НЕ является бесконечной величиной, а вполне конечна и вычисляема.
V>Например, ЧД Стрелец А, масса ~4.3*106 солнечных или 8.6*1036 кг.
V>Радиус Г.С.:R=2MG/c2
V>Ускорение свободного падения на Г.С.:g=MG/R2
Как ты получил этот результат? По формулам ньютоновской гравитации? Это неправильно, они неприменимы для ЧД.
В ОТО есть понятие поверхностной гравитации. Для решения Шварцшильда на горизонте это что-то вроде c^2 / 4GM.
V>Например, мы находимся на 1 тыс км над горизонтом этой ЧД, пусть наш волшебный трос будет 2 тыс км, т.е. датчик нырнул за горизонт на 1 тыс км.
V>С точностью до 3-го порядка вес тела на такой "глубине" при упомянутой скорости вращения будет всего в ~28.3 раза больше земного. Это более чем конечные числа.
V>Что помешает вытянуть такой датчик обратно? ))
Геометрия пространства-времени помешает. Ты с ОТО совсем-совсем не знаком?
DM>>Во-вторых, в ОТО в метрике Шварцшильда двигаться по круговой орбите со скоростью света получится только на радиусе 1.5R, т.е. отнюдь не на горизонте, а в полтора раза дальше.
V>Ты, наверно, имеешь ввиду первую космическую?
V>Тогда не 1.5R, а sqrt(2)R, т.е. ~1.42*R.
Нет, я имею в виду решения ОТО про геодезические для света. См. https://en.wikipedia.org/wiki/Photon_sphere
Не надо ньютоновские формулы для ЧД продолжать использовать, это фейспалм.
DM>>Это популярная ошибка — объяснять горизонт второй космической.
V>А можно несколько ссылок на развенчание этой "ошибки", если она такая популярная?
Постараюсь найти что-то конкретное, а то пока хочется просто послать к любому учебнику по ОТО.
DM>>Там совсем другой механизм. Там другое притяжение: ньютоновская гравитация и ОТО отличаются численно вблизи массивных тел, там формула гравитационного потенциала разная, в ОТО гравитация "сильнее".
V>При чём тут вообще ньютоновская гравитация?
V>Давай оставаться в рамках ОТО.
Вот именно, давай.
V>Насчёт в "ОТО гравитация сильнее" — это зависит от массы ЧД, вернее, от радиуса её горизонта событий.
Числа зависят да, но важно, что есть качественная разница: реально отличаются формулы и траектории. Ты не получишь правильные траектории для движения света и материальных тел вблизи ЧД и просто массивных звезд, пользуясь ньютоновскими формулами.



см. https://en.wikipedia.org/wiki/Schwarzschild_geodesics
V>Ну и, релятивистское увеличение массы не сказывается на ускорении свободного падения.
Это здесь вообще не при чем.
DM>>Или бросить камень с горизонта вверх, он бы подлетел на некоторую высоту над горизонтом и упал бы обратно. Как это работает в ньютоновской гравитации. Но в ОТО это работает иначе, там камень не взлетит с горионта ни на сколько, и даже свет не взлетит.
V>Верно, бо вторая космическая там равна скорости света.
V>Причём, во всех абсолютно направлениях.
V>(с точностью до описани происходящего в случае эллиптического движения)
Подожди пока с направлениями. Тут принципиальный момент: можно ли с горизонта подбросить камень хоть на метр? В ньютоновской механике — можно. В ОТО — нельзя. Ты пока никак не увидишь разницу, похоже, а она важная.
DM>>Камень будет всегда падать вниз, а свет или упадет, или в лучшем случае (будучи пущен строго вверх) останется на горизонте.
V>Строго по касательной если — тоже останется на горизонте (предположим, мы говорим о пределе справа, т.е. сколь угодно близки к горизонту снаружи).
Нет, свет, пущенный ниже фотонной сферы горизонтально, не будет крутиться по орбите и не будет оставаться на горизонте. Он упадет в ЧД.
Тут надо хоть один учебник по ОТО открыть. Мне сложно дать более конкретную ссылку сейчас, чтобы было доходчиво.