Сообщение Re[11]: О несимметричных процессах (что мешает обратить врем от 16.02.2018 4:27
Изменено 16.02.2018 4:29 D. Mon
Re[11]: О несимметричных процессах (что мешает обратить время
Здравствуйте, loginx, Вы писали:
DM>>Как это? Вот есть у нас одна частица, мы измеряем ее положение. Квадрат волновой ф-и дает нам вероятность обнаружить эту частицу в каждой точке пространства. Измерив положение, мы получим одно значение, одну точку.
>>>При этом 1) состояние частицы изменится, 2) волновая ф-я сколлапсирует.
L>погоди, погоди, разве из первого следует второе?!
Нет, скорее 1) это результат 2).
Один из базовых моментов "простой" квантовой механики (предшествовавшей КТП) это то, что при измерении какой-то величины вектор состояния меняется на один из собственных векторов оператора того, что меряем, а измеренное значение — собственное значение, соответствующее этому собственному вектору. Т.е. сам акт измерения это резкое изменение волновой ф-ии. Был у нас какой-то вектор в бесконечномерном пространстве, а осталась одна из его проекций.
L>разве если мы перестанем аблюдать-измерять-положение разве волновая ф-ия не вернется в состояние НЕ-сколлапсирована?
Это будет уже какое-то новое состояние, в которое она сэволюционирует из "схлопнутого". Узнать исходное состояние это нам не поможет.
L>поясни, а что от фазы распределение никак не зависит? фазу никак не измерить? от нее вообще ничего не зависит?
L>Да существует ли фаза если она ни на что никогда не влияет и потому неизмерима?
Фаза, точнее даже разница фаз в разных точках, влияет на поведение волновой функции и на значения многих параметров.
Например, у вот таких двух ВФ

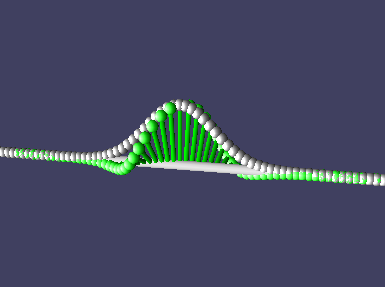
амплитуды одинаковые во всех точках, т.е. распределение вероятностей позиции одно и то же, но вот импульсы у них противоположны (это видно по тому, что закручены они в разные стороны), и при эволюции по ур. Шрёдингера двигаться такие частицы будут в противоположные стороны — первая поползет вправо, вторая влево.
Вот тут подробнее о роли фазы: https://thedeemon.livejournal.com/113053.html
При этом важно именно отличие фаз в разных точках. Если мы всю волновую ф-ю возьмем и повернем в комплексной плоскости на один угол, т.е. умножим на e^ik, то это будет физически то же самое состояние. Это такая базовая глобальная симметрия — выбор нулевой фазы для всей ВФ не играет роли, и в учебниках часто так и пишут, что одному состоянию соответствует не просто вектор в Гильбертовом пространстве, а луч — сколько не умножай на константу, это все одно состояние.
А вот если нулевую фазу в разных точках по-разному выбирать, локально, и потребовать там тоже симметрии, то надо будет производные скорректировать дополнительным полем, это получится поле фотонов, так мы быстро придем к электродинамике.
>>>Волновая функция экспериментами не измерима.
L>модуль то измерится... часть все же измерима?
Часть да, но вот целиком — нет. Это как по проекции вектора на одну ось угадывать исходный вектор. Только осей бесконечно много.
DM>>Как это? Вот есть у нас одна частица, мы измеряем ее положение. Квадрат волновой ф-и дает нам вероятность обнаружить эту частицу в каждой точке пространства. Измерив положение, мы получим одно значение, одну точку.
>>>При этом 1) состояние частицы изменится, 2) волновая ф-я сколлапсирует.
L>погоди, погоди, разве из первого следует второе?!
Нет, скорее 1) это результат 2).
Один из базовых моментов "простой" квантовой механики (предшествовавшей КТП) это то, что при измерении какой-то величины вектор состояния меняется на один из собственных векторов оператора того, что меряем, а измеренное значение — собственное значение, соответствующее этому собственному вектору. Т.е. сам акт измерения это резкое изменение волновой ф-ии. Был у нас какой-то вектор в бесконечномерном пространстве, а осталась одна из его проекций.
L>разве если мы перестанем аблюдать-измерять-положение разве волновая ф-ия не вернется в состояние НЕ-сколлапсирована?
Это будет уже какое-то новое состояние, в которое она сэволюционирует из "схлопнутого". Узнать исходное состояние это нам не поможет.
L>поясни, а что от фазы распределение никак не зависит? фазу никак не измерить? от нее вообще ничего не зависит?
L>Да существует ли фаза если она ни на что никогда не влияет и потому неизмерима?
Фаза, точнее даже разница фаз в разных точках, влияет на поведение волновой функции и на значения многих параметров.
Например, у вот таких двух ВФ


амплитуды одинаковые во всех точках, т.е. распределение вероятностей позиции одно и то же, но вот импульсы у них противоположны (это видно по тому, что закручены они в разные стороны), и при эволюции по ур. Шрёдингера двигаться такие частицы будут в противоположные стороны — первая поползет вправо, вторая влево.
Вот тут подробнее о роли фазы: https://thedeemon.livejournal.com/113053.html
При этом важно именно отличие фаз в разных точках. Если мы всю волновую ф-ю возьмем и повернем в комплексной плоскости на один угол, т.е. умножим на e^ik, то это будет физически то же самое состояние. Это такая базовая глобальная симметрия — выбор нулевой фазы для всей ВФ не играет роли, и в учебниках часто так и пишут, что одному состоянию соответствует не просто вектор в Гильбертовом пространстве, а луч — сколько не умножай на константу, это все одно состояние.
А вот если нулевую фазу в разных точках по-разному выбирать, локально, и потребовать там тоже симметрии, то надо будет производные скорректировать дополнительным полем, это получится поле фотонов, так мы быстро придем к электродинамике.
>>>Волновая функция экспериментами не измерима.
L>модуль то измерится... часть все же измерима?
Часть да, но вот целиком — нет. Это как по проекции вектора на одну ось угадывать исходный вектор. Только осей бесконечно много.
Re[11]: О несимметричных процессах (что мешает обратить врем
Здравствуйте, loginx, Вы писали:
DM>>Как это? Вот есть у нас одна частица, мы измеряем ее положение. Квадрат волновой ф-и дает нам вероятность обнаружить эту частицу в каждой точке пространства. Измерив положение, мы получим одно значение, одну точку.
>>>При этом 1) состояние частицы изменится, 2) волновая ф-я сколлапсирует.
L>погоди, погоди, разве из первого следует второе?!
Нет, скорее 1) это результат 2).
Один из базовых моментов "простой" квантовой механики (предшествовавшей КТП) это то, что при измерении какой-то величины вектор состояния меняется на один из собственных векторов оператора того, что меряем, а измеренное значение — собственное значение, соответствующее этому собственному вектору. Т.е. сам акт измерения это резкое изменение волновой ф-ии. Был у нас какой-то вектор в бесконечномерном пространстве, а осталась одна из его проекций.
L>разве если мы перестанем аблюдать-измерять-положение разве волновая ф-ия не вернется в состояние НЕ-сколлапсирована?
Это будет уже какое-то новое состояние, в которое она сэволюционирует из "схлопнутого". Узнать исходное состояние это нам не поможет.
L>поясни, а что от фазы распределение никак не зависит? фазу никак не измерить? от нее вообще ничего не зависит?
L>Да существует ли фаза если она ни на что никогда не влияет и потому неизмерима?
Фаза, точнее даже разница фаз в разных точках, влияет на поведение волновой функции и на значения многих параметров.
Например, у вот таких двух ВФ


амплитуды (сереньким показанные) одинаковые во всех точках, т.е. распределение вероятностей позиции одно и то же, но вот импульсы у них противоположны (это видно по тому, что закручены они в разные стороны), и при эволюции по ур. Шрёдингера двигаться такие частицы будут в противоположные стороны — первая поползет вправо, вторая влево.
Вот тут подробнее о роли фазы: https://thedeemon.livejournal.com/113053.html
При этом важно именно отличие фаз в разных точках. Если мы всю волновую ф-ю возьмем и повернем в комплексной плоскости на один угол, т.е. умножим на e^ik, то это будет физически то же самое состояние. Это такая базовая глобальная симметрия — выбор нулевой фазы для всей ВФ не играет роли, и в учебниках часто так и пишут, что одному состоянию соответствует не просто вектор в Гильбертовом пространстве, а луч — сколько не умножай на константу, это все одно состояние.
А вот если нулевую фазу в разных точках по-разному выбирать, локально, и потребовать там тоже симметрии, то надо будет производные скорректировать дополнительным полем, это получится поле фотонов, так мы быстро придем к электродинамике.
>>>Волновая функция экспериментами не измерима.
L>модуль то измерится... часть все же измерима?
Часть да, но вот целиком — нет. Это как по проекции вектора на одну ось угадывать исходный вектор. Только осей бесконечно много.
DM>>Как это? Вот есть у нас одна частица, мы измеряем ее положение. Квадрат волновой ф-и дает нам вероятность обнаружить эту частицу в каждой точке пространства. Измерив положение, мы получим одно значение, одну точку.
>>>При этом 1) состояние частицы изменится, 2) волновая ф-я сколлапсирует.
L>погоди, погоди, разве из первого следует второе?!
Нет, скорее 1) это результат 2).
Один из базовых моментов "простой" квантовой механики (предшествовавшей КТП) это то, что при измерении какой-то величины вектор состояния меняется на один из собственных векторов оператора того, что меряем, а измеренное значение — собственное значение, соответствующее этому собственному вектору. Т.е. сам акт измерения это резкое изменение волновой ф-ии. Был у нас какой-то вектор в бесконечномерном пространстве, а осталась одна из его проекций.
L>разве если мы перестанем аблюдать-измерять-положение разве волновая ф-ия не вернется в состояние НЕ-сколлапсирована?
Это будет уже какое-то новое состояние, в которое она сэволюционирует из "схлопнутого". Узнать исходное состояние это нам не поможет.
L>поясни, а что от фазы распределение никак не зависит? фазу никак не измерить? от нее вообще ничего не зависит?
L>Да существует ли фаза если она ни на что никогда не влияет и потому неизмерима?
Фаза, точнее даже разница фаз в разных точках, влияет на поведение волновой функции и на значения многих параметров.
Например, у вот таких двух ВФ


амплитуды (сереньким показанные) одинаковые во всех точках, т.е. распределение вероятностей позиции одно и то же, но вот импульсы у них противоположны (это видно по тому, что закручены они в разные стороны), и при эволюции по ур. Шрёдингера двигаться такие частицы будут в противоположные стороны — первая поползет вправо, вторая влево.
Вот тут подробнее о роли фазы: https://thedeemon.livejournal.com/113053.html
При этом важно именно отличие фаз в разных точках. Если мы всю волновую ф-ю возьмем и повернем в комплексной плоскости на один угол, т.е. умножим на e^ik, то это будет физически то же самое состояние. Это такая базовая глобальная симметрия — выбор нулевой фазы для всей ВФ не играет роли, и в учебниках часто так и пишут, что одному состоянию соответствует не просто вектор в Гильбертовом пространстве, а луч — сколько не умножай на константу, это все одно состояние.
А вот если нулевую фазу в разных точках по-разному выбирать, локально, и потребовать там тоже симметрии, то надо будет производные скорректировать дополнительным полем, это получится поле фотонов, так мы быстро придем к электродинамике.
>>>Волновая функция экспериментами не измерима.
L>модуль то измерится... часть все же измерима?
Часть да, но вот целиком — нет. Это как по проекции вектора на одну ось угадывать исходный вектор. Только осей бесконечно много.