 Оценка 81
Оценка 81 
 Оценить
Оценить 






 Оценка 81 Оценка 81   Оценить Оценить       
|
Не берусь судить. Вероятно, задача о том, как максимально быстро возвести действительное положительное число в произвольную действительную степень, решалась примерно столь же часто, как и вставала, - а вставала, полагаю, не раз. И все же не так давно я с ужасом обнаружил, что RTL из состава Borland Delphi последних версий (как Delphi 6, так и Delphi 7) подходит к решению не более профессионально, чем прилежный пятиклассник, впервые столкнувшийся с такой проблемой.
Взглянем на исходный код функции Power из модуля Math, любезно предоставленный Borland Software:
function Power(const Base, Exponent: Extended): Extended; begin if Exponent = 0.0 then Result := 1.0 { n**0 = 1 } else if (Base = 0.0) and (Exponent > 0.0) then Result := 0.0 { 0**n = 0, n > 0 } else if (Frac(Exponent) = 0.0) and (Abs(Exponent) <= MaxInt) then Result := IntPower(Base, Integer(Trunc(Exponent))) else Result := Exp(Exponent * Ln(Base)) end; |
Примечательно, что в благих целях оптимизации процессор оставляют наедине с целой толпой ветвлений, приводящих его, в конце концов, в общем случае к пресловутому решению пятиклассника, а именно, к тривиальной формуле
(1) x**y = exp(ln(x**y)) = exp(y*ln(x)).
Здесь x**y означает возведение x в степень y, a exp(x) = e**x.
Что плохого в таком подходе к решению? Во-первых, в набор инструкций FPU не входит ни операция вычисления exp(x), ни взятия натурального логарифма ln(x). Соответственно, результат вычисляется в несколько этапов, в то время как можно пойти более прямым путем, как будет показано ниже. За счет этого падает скорость вычисления; кроме того, здесь действует интуитивное правило, которое грубо можно сформулировать так: чем больше операций выполняется над числом с плавающей запятой в регистрах сопроцессора, тем больше будет и суммарная погрешность результата.
| ПРИМЕЧАНИЕ Позднейшая проверка показала, что как Visual C из Visual Studio .NET, так и C++ Builder 4.5 реализуют возведение в степень более качественно. Используемый в них вариант концептуально не отличается от того решения, которое я хочу предложить. |
Давайте проведем инвентаризацию. Какие инструкции сопроцессора связаны с возведением в степень или взятием логарифма? Приведу краткую выдержку из [1] и [2]:
Вот, в общем-то, и все. Но уже на первый взгляд этого хватает, чтобы понять, что задача может быть решена более прямо, чем предлагает RTL Borland Delphi.
Действительно, почему не заменить показатель степени в (1) на 2? Ведь неперово число отнюдь не является родным для двоичной арифметики! Тогда получится
(2) x**y = 2**log2(x**y) = 2**(y*log2(x)).
Это выражение для x**y в соответствии с вышеозначенными пятью инструкциями можно представить как композицию функций в таком виде:
(3) f(z)=2**z,
(4) g(x,y)=y*log2(x),
(5) xy =f(g(x,y)).
Так как вычислить f(z) в одно действие невозможно, приходится считать так:
(6) f(z)=2**z=2**(trunc(z)+(z-trunc(z)))=(2**trunc(z)) * (2**(z-trunc(z))).
Формулы (4)-(6) естественно выражаются таким ассемблерным кодом:
;Во-первых, вычисляем z=y*log2(x): fld y ;Загружаем основание и показатель степени fld x fyl2x ;Стек FPU теперь содержит: ST(0)=z ;Теперь считаем 2**z: fld st(0) ;Создаем еще одну копию z frndint ;Округляем fsubr st(0),st(1) ;ST(1)=z, ST(0)=z-trunc(z) f2xm1 ;ST(1)=z, ST(0)=2**(z-trunc(z))-1 fld1 faddp ;ST(1)=z, ST(0)=2**(z-trunc(z)) fscale ;ST(1)=z, ST(0)=(2**trunc(z))*(2**(z-trunc(z)))=2**t fxch st(1) fstp st ;Результат остается на вершине стека ST(0) |
| ПРЕДУПРЕЖДЕНИЕ Перед выполнением этого фрагмента кода нужно убедиться, что биты управления округлением в слове управления FPU установлены в режим округления к нулю. В Delphi это проще всего сделать при помощи функции SetRoundMode (модуль Math): SetRoundMode(rmTruncate); |
| ПРИМЕЧАНИЕ Так как на процессорах Intel Pentium IV последовательное многократное переключение между двумя (но не более) состояниями слова управления FPU выполняется гораздо быстрее, чем на ранних моделях, можно рассчитывать, что даже в тех ситуациях, когда придется перемежать вызов этого фрагмента кода с действиями, требующими иного режима округления, при работе на современной технике это не приведет к чрезмерным дополнительным временным затратам. Подробности см., например, в [3]. |
Полный код работоспособной функции на Object Pascal выглядит так:
function _Power(const x,y:FLOATTYPE):FLOATTYPE; //x>0! asm fld y fld x fyl2x fld st(0) frndint fsubr st(0),st(1) f2xm1 fld1 faddp fscale fxch st(1) fstp st end; |
| СОВЕТ Имеет смысл создать перегруженные версии функции для различных типов аргументов FLOATTYPE, так как на практике часто главным недостатком встроенной функции является то, что она (как и все вызываемые ею функции) принимает в качестве аргументов действительные числа типа Extended, что приводит к весьма существенным затратам на конвертирование форматов при загрузке в стек FPU. |
Эксперименты показали, что предложенный вариант функции возведения в степень повышает точность вычислений на один-два знака после запятой. Так как автору было несколько лень писать медленный код для сверхточного возведения в степень с целью проверки точности предложенного алгоритма, то эксперимент заключался в сравнении результатов со значением, получающемся в стандартном калькуляторе Windows. Если верить его справочной службе, вычисления в нем производятся с точностью до 32 десятичных знаков после запятой, что позволяет полагаться на него как на источник эталонных значений.
К сожалению, выигрыш в скорости абсолютно не ощущается. Это вполне объяснимо: согласно приложению C (“IA-32 Instruction Latency and Throughput”) документа [3], из всего этого фрагмента основная вычислительная нагрузка ложится на трансцендентные (ответственность за не вполне корректное применение термина ложится не на меня, а на господ из Intel) операции, а именно – FYL2X, FRNDINT, F2XM1 и FSCALE. Количество же этих операций в предложенном алгоритме и их общее число в реализации функций ln(x) и exp(x) в RTL Delphi одинаково.
Конечно, хотелось бы увеличить и скорость вычислений. Но мир не идеален, и за это придется расплачиваться все той же точностью. Как правило, в каждой ситуации существует предел допустимых погрешностей при расчетах. В иллюстративных целях я задался максимальной допустимой относительной погрешностью 0,0001=0,1%. В действительности, как будет видно из графиков относительной погрешности, удалось достичь еще большей точности.
Дальнейшие наши действия должны состоять в том, чтобы исключить трансцендентные математические операции. Ясно, что всякое представление в виде конечной композиции элементарных арифметических операций некоторой функции, неразложимой в такую композицию, является приближением исходной функции. То есть задача ставится так: нужно приблизить используемые трансцендентные функции композициями элементарных операций, оставаясь при этом в допустимых для погрешности пределах.
Эта мера позволит нам избавиться сразу и от длительной F2XM1, и от выполняющейся ненамного быстрее FSCALE.
Существует бесконечное множество способов приблизить функцию f(x). Один из наиболее простых в вычислительном плане – подбор подходящего по точности многочлена g(x)=anxn+an-1xn-1+...+a1x+a0. Его коэффициенты могут быть постоянны, а могут некоторым образом зависеть от x. В первом случае коэффициенты легко найти методом наименьших квадратов, взяв значения исходной функции в нескольких точках и подобрав коэффициенты так, чтобы в этих точках многочлен принимал значения, как можно более близкие к значениям функции (подробное описание полиномиальной аппроксимации функций и метода наименьших квадратов можно найти в книгах, посвященных курсам вычислительной математики или обработке экспериментальных данных). Простота метода оборачивается существенным недостатком: он подчас неплох для выявления качественных тенденций, но плохо отражает исходную функцию количественно, причем, как правило, погрешность растет с уменьшением степени многочлена n, а скорость вычисления g(x) с ростом n падает.
Достойная альтернатива, позволяющая достаточно точно приближать гладкие кривые, такие, как y=2**x, - аппроксимация сплайнами. Говоря простым языком (возможно, чересчур простым – пусть меня извинят специалисты), сплайн – это кривая, моделирующая форму, принимаемую упругим стержнем, деформированным путем закрепления в заданных точках. Она проходит точно через заданные точки, подчиняясь при этом некоторым дополнительным условиям, в частности, условию непрерывности второй производной. Существуют различные виды сплайнов. В этой работе достаточно практично использование кубических сплайнов. Кубический сплайн на каждом отрезке между двумя последовательными (в порядке возрастания координаты x) эталонными точками (x,f(x)) описывается полиномом третьей степени g(x)=a3x3+a2x2+a1x+a0, где набор коэффициентов (a0,a1,a2,a3) свой для каждого отрезка. Поиск этих коэффициентов – не слишком сложная задача, но описание метода ее решения выходит за рамки этой статьи. Таблица коэффициентов, получающаяся после учета всех замечаний этого раздела, прилагается к статье.
Итак, я ограничусь лишь использованием полученных мною значений коэффициентов. Чтобы обеспечить необходимую точность на промежутке 0<=x<999, мне понадобились в качестве эталонных 2039 точек, которым соответствовали значения x=(i-40)/2, i=0..2038. Сорок значений на отрицательной полуоси нужны были только для того, чтобы отразить поведение сплайна в этой части плоскости, слегка скорректировав таким образом его вид на остальных отрезках; в вычислениях эти 40 отрезков не участвуют, т.к. для значений x<0 можно воспользоваться (без ощутимого проигрыша в скорости или точности) соотношением 2**(-|x|)=1/(2**|x|).
Итак, у нас есть таблица коэффициентов, представленная в виде массива из 1999 блоков по 8*4 байт (если для представления коэффициентов используется тип double). На Object Pascal такой массив описывается типом
array [0..1998] of packed record c3,c2,c1,c0:double end; |
На практике возникает тонкий момент. Дело в том, что Delphi почему-то отказывается выравнивать массивы Double’ов по границе 8 байт. Лично у меня получается так, что адрес первого элемента всегда бывает кратен 4, но никогда – 8. Поэтому перед началом массива я вставляю заполнитель, чтобы избежать медленного чтения некоторых double’ов, которые частично лежат в одной 64- или 32-байтной линейке кэша, а частично – в следующей:
//Предполагаю, что выставлена опция компилятора {$Align 8} Type TArr=packed record Padding:integer; //Фиктивный 4-байтовый заполнитель - чтобы массив выравнялся по 8 байтам C:array [0..1998] of packed record c3,c2,c1,c0:double end; //Собственно коэффициенты end; |
На вход функции Exp2 поступает единственный аргумент x - возводимое в степень число. Как можно реализовать функцию?
Вот как это сделал я.
| ПРЕДУПРЕЖДЕНИЕ Как и для предыдущей функции, нужно обеспечить установку бит управления округлением в режим округления к нулю. |
function Exp2(x:FLOATTYPE):FLOATTYPE; //0<=x<999 asm fld x call Core_Exp2 //Оформим основную часть в виде процедуры, т.к. она будет использоваться не только здесь - // - да и перегрузку функций для другого типа аргумента так делать удобнее. end; procedure Core_Exp2; //На вершине стека FPU находится аргумент var i:integer; //Сюда получим индекс в массиве asm fld st //Копируем аргумент fadd st,st //st(1)=x, st(0)=2x fistp i //Достаем i (индекс равен trunc(2x)); st(0)=x fild i //Полагаемся на т.н. Store-Forwarding: округленное значение передается сразу инструкции // fild, не ожидая, пока данные будут записаны в память; st(1)=x, st(0)=trunc(2x) mov eax,i fld1 //st(2)=x, st(1)=trunc(2x), st(0)=1 lea eax,[eax*4] //То есть eax:=i*4 add eax,eax // *2 add eax,1 // +1 = i*8+1 (далее при доступе к массиву используется eax*4, то есть i*32+4, // т.к. каждая строка по 4*8=32 байта и заполнитель в начале – 4 байта. // Если бы не было заполнителя, последнюю инструкцию нужно было бы убрать. fadd st,st fld1 fdivrp //=0.5 fmulp //st(1)=x, st(0)=0.5*trunc(2x) fsubp //st(0)=dx //Подсчет по схеме Горнера. Мне казалось, что можно сделать это быстрее, //пустив параллельно несколько цепочек вычислений, но пока это не удалось сделать. fld qword ptr coeffspow[4*eax] fmul st,st(1) fld qword ptr coeffspow[4*eax+8] faddp fmul st,st(1) fld qword ptr coeffspow[4*eax+16] faddp fmul st,st(1) fld qword ptr coeffspow[4*eax+24] faddp fxch st(1) fstp st //Освобождаем ненужный регистр end; |
| ПРЕДУПРЕЖДЕНИЕ Выполнение этого фрагмента изменяет содержимое регистра EAX. |
Оценим погрешность приближения. Так как результат, получаемый как _Power(2,x) (функция _Power приведена в начале статьи), заведомо точнее, чем Exp2(x), то в качестве оченки примем относительное отклонение значения последней функции от значения первой: Epsilon=abs( Exp2(x) - _Power(2,x) ) / _Power(2,x). Разумеется, выражение имеет смысл, если _Power(2,x)<>0.
Если построить график относительной погрешности, становится видно, что в пределах каждого из 1998 отрезков он имеет форму кривой с одним максимумом, сходящей к нулю на концах отрезка. При этом пределы колебаний величины погрешности остаются постоянными на всех отрезках, кроме нескольких последних – на них погрешность возрастает. Если не принимать во внимание эти отрезки, и ограничить область допустимых значений аргумента числом 990 (т.е. x<990), то для описания поведения относительной погрешности в зависимости от x достаточно показать ее график на двух последних допустимых для значений x отрезках:
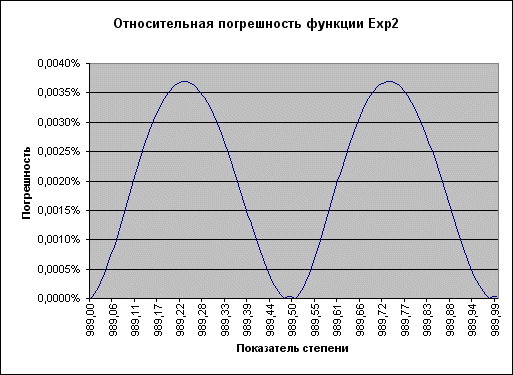
Рисунок 1. Максимальная погрешность приближения функции Exp2=2**x (при x менее 990) не превышает 0,004%.
| СОВЕТ Мы отсекли отрезки, лежащие правее точки x=990. Следовательно, размер таблицы коэффициентов можно несколько сократить: индекс последнего элемента должен быть 990*2=1980, а не 1998. “Лишние” 19 последних строк таблицы можно просто удалить. Логично также изменить текст комментария в начале функции Exp2. |
Изменим реализацию возведения в степень в соответствии с предложенной аппроксимацией для 2**x:
function New_Power(x,y:FLOATTYPE):FLOATTYPE; //abs(y*log2(x))<990 asm fld y fld x fldz //Сравним основание степени fcomip st,st(1) // с 0 и соответственно установим флаги процессора je @Zero FYL2X //Стек: ST(0)=t=y*log2(x) fldz fcomip st,st(1) //Флаги выставляем соответственно числу 0-y*log2(x) ja @Reverse //Если 0>y*log2(x), то сосчитаем 2**|y*log2(x)|, а после инвертируем call Core_Exp2 jmp @Exit @Zero: fxch st(1) fstp st //Освобождаем ненужный регистр jmp @Exit @Reverse: fabs //Берем абсолютную величин call Core_Exp2 fld1 //Считаем обратное значение: fdivrp //1/(2**|y*log2(x)|) @Exit: end; |
| ПРЕДУПРЕЖДЕНИЕ В этом фрагменте используется инструкция FCOMIP, впервые появившаяся на процессорах Pentium Pro. Любителям антиквариата придется использовать вместо пары команд FCOMIP / JE блок |
FCOMP
FSTSW
TEST AX, 16384
JNZ @Zero //Вместо je @Zero
|
| ПРЕДУПРЕЖДЕНИЕ А вместо FCOMIP / JA - блок |
FCOMP FSTSW TEST AX, 256 or 16384 //0<= y*log2(x) ? JZ @Reverse //Нет, случай со взятием обратного значения |
| ПРЕДУПРЕЖДЕНИЕ Вдобавок в этом случае изменяется регистр EAX. |
Результаты тестирования отражены на графиках:
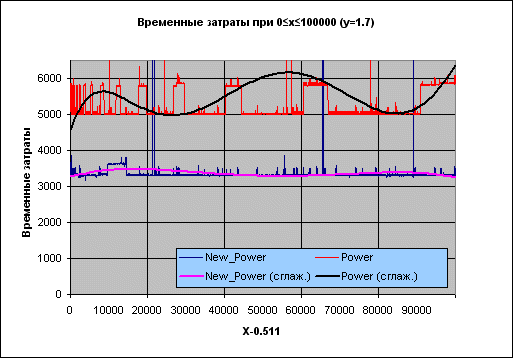
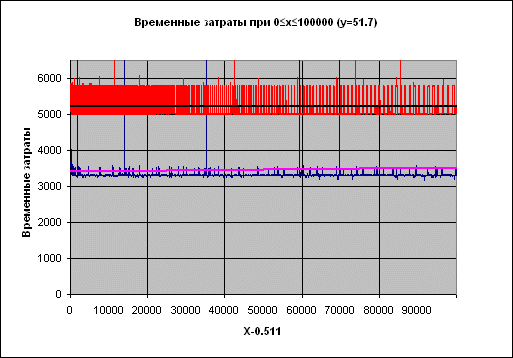
Рисунок 2. Временные затраты: New_Power – новая функция, Power – из состава RTL Borland Delphi.
Подпись X-0.511 на оси абсцисс отражает тот факт, что при проведении испытаний брались значения целые значения X, к которым затем прибавлялось число 0.511, чтобы гарантировать, что основание степени – число нецелое (т.е. чтобы рассматривать по возможности общий случай).
Черная линия поверх красного набора – сглаженные временные затраты функции Power, фиолетовая поверх синего – функции New_Power.
Замеры временных затрат производились с помощью инструкции RDTSC (процессоры начиная с Pentium):
function time:int64; //Вспомогательная функция для подсчета времени работы asm rdtsc end; |
и далее в коде
t:=time(); ... writeln(time()-t); |
RDTSC возвращает в регистровой паре EDX:EAX число тактов процессора, прошедших с момента последнего сброса (reset). Машинный код инструкции – 0Fh, 31h.
Относительная погрешность ведет себя на удивление стабильно, изменяясь в пределах от 0 до 0,0040%. Поэтому достаточно представительным множеством значений аргумента является, к примеру, промежуток (0, 1000).
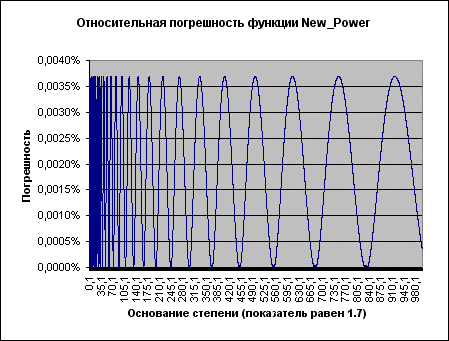
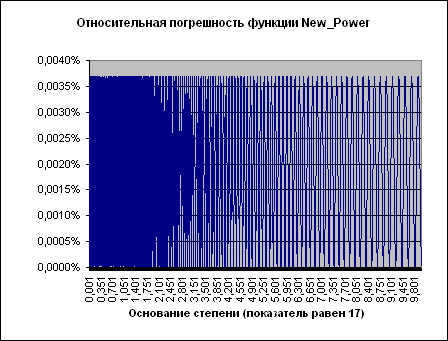
Рисунок 3.
Видно, что оцененная относительная погрешность (фактически - отклонение от значения, возвращаемого встроенной функцией) на самом деле не превосходит 0.004% !
В случае показателя степени 17 колебания становятся намного чаще, однако общая картина та же.
Логарифмирование плохо поддается аппроксимации с помощью кубических сплайнов – точнее, мне удалось это сделать, причем с весьма высокой точностью, но лишь ценой проигрыша по времени в сравнении с использованием FYL2X. Однако здесь есть что предпринять и не прибегая к сплайнам.
Как известно, функция ln(1+x) при |x|<1 разлагается в ряд Тейлора следующим образом:
ln(1+x)=x-x2/(1*2)+x3/(1*2*3)+…+ xi/i!+…
Если абсолютная величина x достаточно мала, члены ряда, уже начиная с третьего, достаточно слабо сказываются на результате. Поэтому для значений x, достаточно близких к 1 (чтобы остаться в оговоренных выше рамках приемлемых погрешностей, x должен отстоять от 1 не больше чем на 0.01), вычисление log2(x)=ln(x)/ln(2)=ln(x)*log2(e)=ln(1+(x-1))*log2(e) можно заменить вычислением (t-t*t/2)*log2(e), где t=x-1.
Это позволяет построить еще один вариант функции возведения в степень для значений основания, близких к 1. В нем нет инструкции FYL2X, а вместо нее присутствует блок инструкций, помеченных символом “ * ” (знак “~” означает приближенное равенство):
function New_Power_XNear1(x,y:FLOATTYPE):FLOATTYPE; // abs(y*log2(x))<990 asm fld y fld x fldz fcomip st,st(1) je @Zero fld1 (*) fsub st(1),st (*) fld st(1) (*) //st(0)=1; st(1)=st(3)=t=x-1, st(2)=1, st(4)=y fld1 (*) fadd st,st (*) fdivp st(2),st (*) //st(0)=st(2)=t, st(1)=1/2, st(3)=y fmul st,st (*) fmulp st(1),st (*) //st(0)=1/2*t*t, st(1)=t, st(2)=y fsubp st(1),st (*) //st(0)=t-t*t/2 ~ ln(x), st(1)=y fldl2e (*) //Загружаем константу log2(e) fmulp (*) //st(0)~log2(x), st(1)=y fmulp (*) //st(0)~y*log2(x) fldz fcomip st,st(1) ja @Reverse call Core_Exp2 jmp @Exit @Zero: fxch st(1) fstp st //Освобождаем ненужный регистр jmp @Exit @Reverse: fabs call Core_Exp2 fld1 fdivrp @Exit: end; |
Таким образом, нам в этом случае (при x, близких к 1) удается избавиться от всех инструкций FPU, принадлежащих к группе трансцендентных, что приводит к впечатляющему росту производительности:
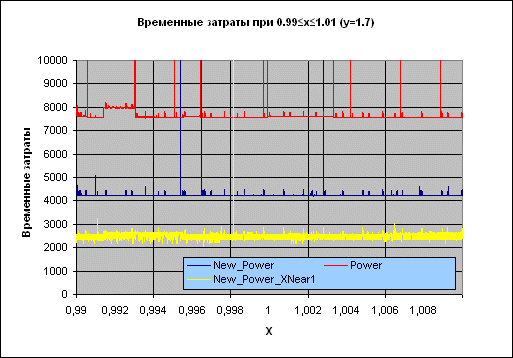
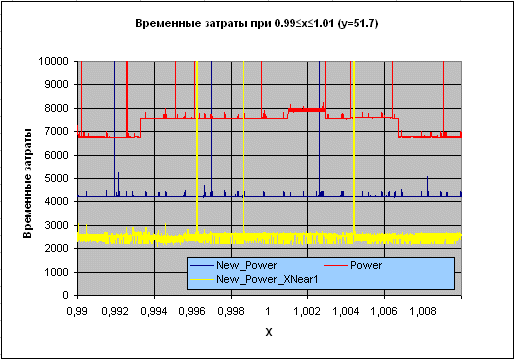
Рисунок 4. Временные затраты: New_Power_XNear1 – специализированный вариант New_Power.
К сожалению, с ростом показателя степени максимальная погрешность растет, оставаясь, впрочем, в оговоренных пределах (т.е. меньше 0,1%; более того – меньше 0,01%) даже при очень больших показателях:
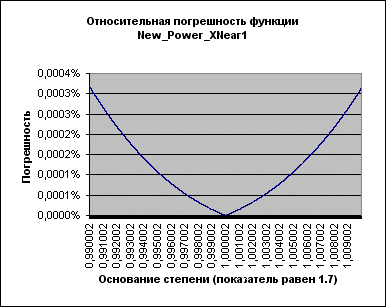
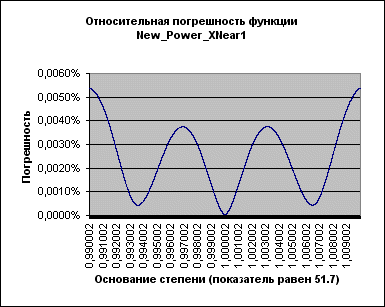
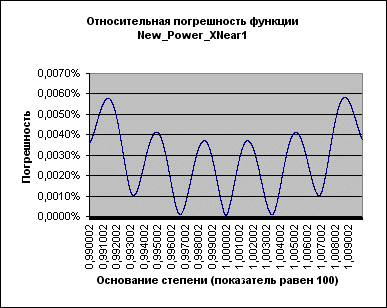
Рисунок 5.
Таким образом, нам удалось получить функции, превосходящие встроенную по скорости от двух до четырех раз при погрешности порядка 0.004% - 0.01%. Не исключено, что существует возможность провести более качественную и более выгодную в смысле временных затрат аппроксимацию функций; возможно, даже по другому принципу, а не так, как это было сделано здесь (т.е. исходя из соотношения x**y=2**(y*log2(x)) ).
Для тех же случаев, когда необходима высокая точность вычислений, в качестве первого камня фундамента была рассмотрена функция, исправляющая недостаток Delphi RTL. Несомненно, это направление также достойно дальнейших исследований с целью ускорить заведомо медленные вычисления с повышенной точностью.
Очень познавательно чтение следующих документов:
 Оценка 81 Оценка 81   Оценить Оценить       
|