Я пишу разные алгоритмы, помогите разобраться.
Есть двумерная карта (x,y и z — глубина), точнее набор точек, надо описать её некой моделью. Проще всего, наверно, построить двумерный полином:
Z=a+bx+cx^2+dx^3+…+gy+hy^2+iy^3+...
Имеем набор коэффициентов a,b,c…,g,h… Их можно подогнать для минимизации среднекрадратичного отличия от исходных значений z каждой точки и рассчитанных согласно модели. Эта задача, как я понял, достаточно простая: мы знаем что в минимуме производная МНК-функционала (сумма квадратов различий исходных данных и рассчитанных) по каждому оптимизируемому коэффициенту равна нулю.
Правда я уже путаюсь, не меняется ли картина при переходе от одномерной модели к двумерной (для одномерной я давно уже делал все эти преобразования, надо найти старый код и вспомнить).
Я думаю, в целом этот подход не особо подходящий, поскольку полином обладает таким свойством – он часто петляет вверх-вниз, особенно на краях функции. Вот пример:



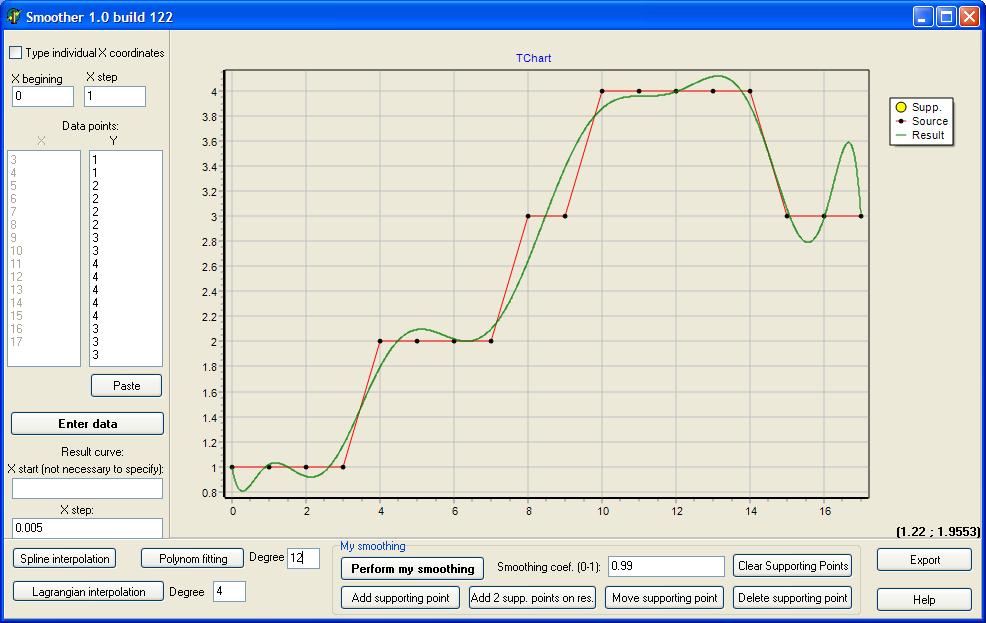
Более правильно, как я понимаю, использовать сплайны: функция разбивается на отдельные участки, каждый описывается степенной функцией, например y=a+bx+cx^2+dx^3.

Вот здесь проводятся сплайны третьей степени между точками (это не аппроксимация а интерполяция):



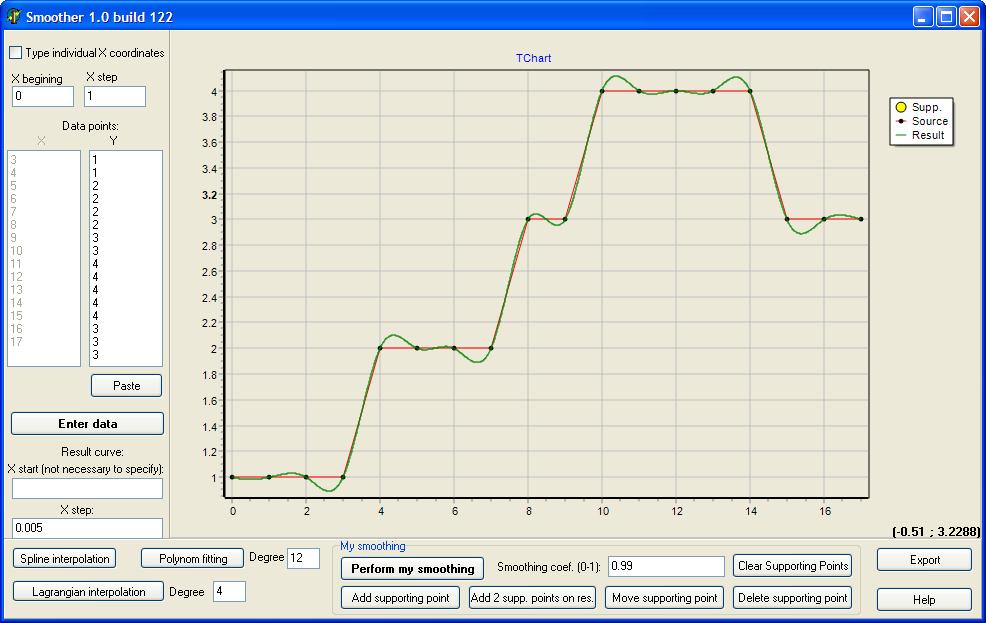
Хотя я сам написал этот код, я его не очень понимаю. Формулы были взяты из книги “Численные методы” (автора не помню). Хочу понять общий смысл этих формул.

Предположим, у нас есть 6 эвкидистантных точек, которые надо интерполировать сплайном. Это значит что у нас 5 интервалов, на каждой из которых проведён свой сплайн.
Мне понятна эта задача, если степень сплайна равна двум: y=a+bx+cx^2. Значит в данном случае мы имеем 5*3=15 коэффициентов, которые надо найти. В каждом интервале мы знаем два значения сплайна (слева и справа), это уже 5*2=10 уравнений. Ещё мы знаем, что для четырёх граничных точек первые производные сплайна слева и сплайна справа совпадают, соответственно имеем ещё 4 уравнения. Чтобы довести число уравнения до числа коэффициентов (15), нужно добавить ещё одно, например такое: для самого левого сплайна первая производная в его левой границе равна производной в правой границе. Действительно, ведь если мы имеем всего 2 точки и один интервал, то сплайн второй степени можно провести бесконечным числом способов, т.е. надо ещё добавить какое-то условие.
В моей же программе, в которой взяты формулы из книги “Численные методы”, сплайн не второй, а третьей степени. Значит, коэффициентов, которые нужно найти, в 4/3 раза больше, т.е. надо добавить ещё уравнений. Я тут не очень понимаю – каких именно? Может быть, нужно ещё минимизировать интеграл от квадрата второй производной всей функции?

А когда я буду переходить от одномерной задачи к двумерной, тут вообще получается тёмный лес. Кажется есть “би-сплайны” которыми надо аппроксимировать данные (не путать с B-сплайном), но в Вики вроде нет по ним статьи. А я вообще запутался даже с самим простым вариантом этой задачи – элементарная линейная интерполяция.

Интерполяция – вещь вроде понятная. На рисунках красная линия – это собственно линейная интерполяция. Для одномерной задачи между двумя точками просто проводится отрезок. Можно подумать, что в двумерной задаче можно провести плоскость в каждом квадрате, на который разбито пространство, но вот нет: плоскость описывается тремя точками, а на границах квадрата есть четыре точки.