 Оценка 181
Оценка 181 
 Оценить
Оценить 






 Оценка 181 Оценка 181   Оценить Оценить       
|
| Введение Accelerator v2 Brahma TidePowerd GPU.NET Сравнение результатов Выводы Список литературы |  |
Архитектура современных графических процессоров позволяет эффективно выполнять паралелльные вычисления. Графический процессор, в отличие от универсального, обладает меньшим набором исполняемых команд, но большей производительностью. В последние несколько лет графический процессор стали активно применять не только для решения специализированных задач (обработка графической информации), но и для вычислений общего назначения. Данная техника называется GPGPU.
Основные производители видеочипов NVIDIA и AMD разработали соответствующие платформы под названием CUDA (Compute Unified Device Architecture) и CTM (Close To Metal или AMD Stream Computing). Обе платформы предоставляют программисту прямой доступ к аппаратным возможностям видеокарты, но требуют от него определенного уровня знаний особенностей технологии. Помимо данных платформ существуют библиотеки, предоставляющие более высокоуровневый доступ к параллельным вычислениям, которые для этого используют API DirectX и OpenGL. Подобные библиотеки позволяют начать использование графического процессора здесь и сейчас, и не требуют от разработчика затрат времени на изучение технологии. В статье будет рассмотрено использование библиотек Accelerator v2, Brahma и TidePowerd GPU.NET. Целью статьи является определение наиболее подходящей библиотеки для проведения операции умножения матрицы на вектор в рамках диссертационной работы автора.
Accelerator v2 позволяет ускорять вычисления как на многоядерном центральном процессоре, так и на графическом. Библиотека распространяется под лицензией MSR-LA, которая разрешает только некоммерческое использование. Проект разрабатывается в Microsoft Research, поэтому после релиза, скорей всего, лицензия будет изменена. Сама библиотека создана на языке С++, но с ней поставляется и специальная обертка, написанная на управляемом коде. Область применения ограничивается доступностью DirectX, с помощью которого и производится ускорение на GPU. Важно отметить, что для работы требуется совместимая с DirectX 9 видеокарта. Другое ограничение касается выполнения расчетов на многоядерных центральных процессорах – оно доступно только для 64-битных систем. После установки нужно добавить ссылку на сборку Microsoft.Accelerator.dll и скопировать поставляемую нативную библиотеку Accelerator.dll в папку с проектом.
В качестве задачи была выбрана операция умножения матрицы величины NxN на вектор размером N, где N достаточно велико, например, больше 4096.
Саму процедуру выполнения вычислений средствами графического процессора можно описать следующим образом:
Библиотека Accelerator не оперирует обычными массивами, для этого существует специальный тип ParallelArray. От него наследуются конкретные типы массивов в зависимости от данных – это может быть BoolParallelArray, DoubleParallelArray, FloatParallelArray, IntParallelArray или Float4ParallelArray. Для простоты кода будут использоваться следующие сокращения:
using FPA = Microsoft.ParallelArrays.FloatParallelArray;
using PA = Microsoft.ParallelArrays.ParallelArrays; |
Зададим исходные массивы данных (матрицу и скаляр) и заполним их случайным данными:
int len = 4096;
Random ranGen = new Random(42);
float[,] matrix = newfloat[len, len];
float[] vector = newfloat[len];
float[] result = newfloat[len];
for (int i = 0; i < len; i++)
{
for (int j = 0; j < len; j++)
matrix[i, j] = (float)ranGen.NextDouble(float.MaxValue);
vector[i] = (float)ranGen.NextDouble(float.MaxValue);
} |
| ПРИМЕЧАНИЕ Преобразование генерируемого случайного значения из типа double во float вынужденное, так как библиотека не смогла произвести вычисления с вещественным числом двойной точности. |
Проведем преобразование массивов к специальному типу ParallelArray:
FPA matrixGpu = new FPA(matrix); FPA vectorGpu = new FPA(vector); |
Воспользуемся готовым методом библиотеки Accelerator для проведения нужной операции и конвертируем результат к обычному виду:
FPA resultGPU = PA.InnerProduct(matrixGpu, vectorGpu); // определим устройство выполнения DX9Target dx9Target = new DX9Target(); result = dx9Target.ToArray1D(vectorGpu); |
Программа умножения матрицы на вектор с помощью графического процессора готова. В приведенном выше коде задается устройство выполнения, которое лучше один раз определить в блоке инициализации. Помимо DX9Target существует значение X64MulticoreTarget, которое предназначено для распараллеливания вычислений на центральном процессоре.
Библиотека предоставляет широкий набор готовых математических и логических операций, число которых превышает число методов стандартной библиотеки Math из одноименного пространства имен .NET Framework. Полный список доступных операций можно найти в [1].
Библиотека Brahma написана для .NET Framework 3.5. С ее помощью можно внутри одного метода легко задействовать и центральный, и графический процессор. Brahma использует синтаксис языка интегрированных запросов (LINQ) для потоковой трансформации данных. Библиотека является кроссплатформенной и распространяется под свободной лицензией. Библиотека позволяет использовать графический процессор как через DirectX, так и через OpenGL.
Чтобы произвести вычисления на графическом процессоре с помощью библиотеки Brahma, необходимо:
Создать провайдер вычислений:
var computationProvider = new ComputationProvider(); |
Преобразовать массивы данных к типу DataParallelArrayBase. В зависимости от порядка массива используется соответствующий класс, наследуемый от DataParallelArrayBase:
var matrixPar = new DataParallelArray2D<float>(computationProvider, matrix);
var vectorPar = = new DataParallelArray<float>(computationProvider, vector); |
Создать код (скомпилированный запрос), который будет выполняться на GPU, с помощью синтаксиса языка интегрированных запросов:
CompiledQuery multiplyMatrixByVector = computationProvider.Compile< DataParallelArray2D<float>, DataParallelArray<float>>( (d1, d2) => from m in d1 from v in d2 select d1[output.CurrentX, output.CurrentY] * d2[output.Current] + d1[output.CurrentX + 1, output.CurrentY] * d2[output.Current] ); |
| ПРИМЕЧАНИЕ В приведенном коде демонстрируется возможность умножения матрицы 2x2 на вектор, состоящий из двух элементов. |
Выполнить код и получить результат
IQueryable result = computationProvider.Run( multiplyMatrixByVector, matrixPar, vectorPar); |
Использование языка интегрированных запросов позволяет быстро определить код, исполняемый на графическом процессоре, однако вместе с этим накладывает ограничения на выполняемые операции. В данном случае в коде запроса нужно явно определить умножаемые элементы массивов, таким образом, умножение матрицы на скаляр средствами Brahma затруднительно. Можно, конечно, представить матрицу как множество скаляров и произвести умножение каждого элемента набора на вектор, но при этом теряется удобство использования.
Несмотря на это ограничение скомпилированного запроса, библиотека, в целом, оставила положительные эмоции – бесплатность, кроссплатформенность, хорошие тестовые примеры и простота использования.
На данный момент библиотека находится в стадии бета-версии, но проект активно развивается. В отличие от остальных средств TidePowerd GPU.NET изначально имеет коммерческую основу. Лицензия на одно место разработчика составляет 2500 долларов, однако помимо самой библиотеки программист получит полноценную техническую поддержку 24/7. GPU.NET неправильно называть только библиотекой, потому что после компиляции проекта в обычную .NET-сборку происходит пост-обработка сборки. Для этого в пост-событие проекта добавляется строчка вида:
"C:\Program Files (x86)\TidePowerd\GPU.NET\TidePowerd.Build.exe" --input "$(TargetPath)" --output "$(TargetPath)" |
Создатели GPU.NET заявляют об автоматической оптимизации кода, рассчитанного на выполнение на графическом процессоре, и тесной интеграции со средой разработки Visual Studio. Помимо этого, GPU.NET является кроссплатформенной технологией.
Использование GPU.NET несколько отличается от использования Accelerator и Brahma. В явном виде определяется метод, который будет выполняться на графическом процессоре с помощью специального атрибута TidePowerd.DeviceMethods.Kernel. К сожалению, на текущий момент доступен всего один пример использования данной библиотеки, сама документация также находится в процессе разработки. При использовании GPU.NET был выявлен недостаток библиотеки – невозможность оперировать с двумерными массивами (пост-обработка выдавала ошибку в этом случае). Чтобы оценить, насколько быстро выполняется операция умножения матрицы на скаляр, код был изменен соответствующим образом – добавлен дополнительный цикл, в котором вектор умножался на другой вектор N число раз, где N – размерность вектора.
[TidePowerd.DeviceMethods.Kernel] privatestaticvoid TidePowerdInternal( int len, float[,] matrix, float[] vector, float[] result) { int threadId = BlockDimension.X * BlockIndex.X + ThreadIndex.X; int totalThreads = BlockDimension.X * GridDimension.X; for (int i = threadId; i < vector.Length; i += totalThreads) for (int j = 0; j < vector.Length; j++) result[i] += vector[i] * vector[j]; } |
Метод TidePowerdInternal обычным образом используется в проекте, таким образом, GPU.NET наилучшим образом подходит для модификации существующего кода – достаточно только переписать код, который должен выполняться на GPU.
Результат выполнения кода с помощью GPU.NET оказался таким же, как и без него. Таким образом, на данном этапе невозможно судить о перспективности библиотеки из-за недостатка документации и примеров, по которым можно было бы сказать, верно ли написано тестовое приложение. Отладка средствами VS невозможна внутри метода, помеченного атрибутом Kernel.
Brahma была исключена из теста умножения матрицы на скаляр, однако поставляемые исходные коды позволяют убедиться в эффективности библиотеки для других задач. Помимо кода для Accelerator и TidePowerd был написан следующий код для выполнения на универсальном процессоре:
for (int i = 0; i < len; i++)
{
for (int j = 0; j < len; j++)
result[i] += matrix[i, j] * vector[j];
} |
Результат выполнения приведен на графике (по оси абцисс отложена размерность массивов, по оси ординат – время выполнения в миллисекундах).
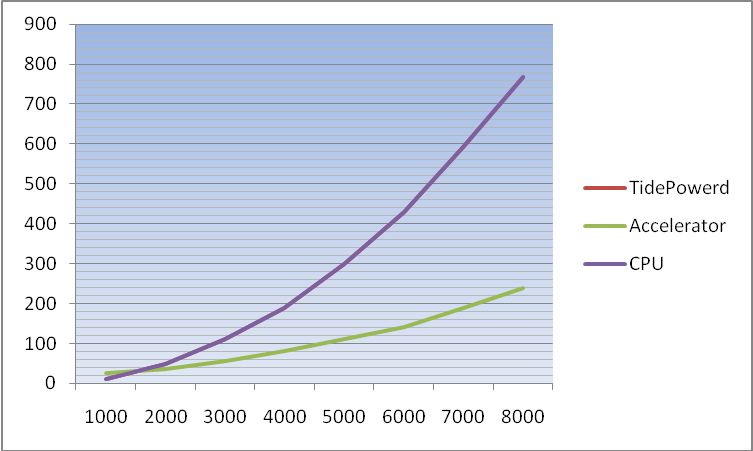
Рисунок 1.
| ПРИМЕЧАНИЕ TidePowerd GPU.NET показал результаты аналогичные выполнению операции на универсальном процессоре. С текущей степенью готовности (недостаток тестовых примеров и документации) библиотека не годится к использованию в проекте. |
Целью тестирования являлась проверка целесообразности использования библиотеки для ускорения расчетов на графическом процессоре в научной работе. По результатам тестирования была выбрана библиотека Accelerator для ускорения выполнения вейвлет-преобразований в дисссертационной работе.
Из-за описанных выше преимуществ библиотека Brahma рекомендуется к использованию в неакадемических проектах. Если требуется обеспечить максимальную производительность на GPU, лучше всего использовать решения от NVidia или AMD, которые позволяют более гибко управлять вычислениями. О проекте GPU.NET можно будет судить только через некоторое время.
 Оценка 181 Оценка 181   Оценить Оценить       
|