 Оценка 15
Оценка 15 
 Оценить
Оценить 






 Оценка 15 Оценка 15   Оценить Оценить       
|
| Процедуры сравнения Последовательный поиск Бинарный поиск Вставка элемента в отсортированный контейнер Резюме |  |
Поиск – это действие, заключающееся в просмотре набора элементов и выделении из этого набора интересующего элемента. Наверное, все вы знакомы с одной из функций поиска – Pos из модуля SysUtils, которая предназначена для поиска подстроки в строке.
Эта и следующая главы, посвященные поиску, довольно-таки тесно связаны между собой. Часто поиск элемента приходится осуществлять в уже отсортированном контейнере. И если контейнер отсортирован, можно воспользоваться эффективным алгоритмом для поиска позиции вставки нового элемента, чтобы и после вставки контейнер оказался отсортированным. Тем не менее, поиск не ограничивается просмотром отсортированных списков. Мы, помимо прочих, рассмотрим простейший тип поиска – алгоритмы, которые кажутся почти очевидными и не заслуживают специального названия.
Кроме того, настоящая глава служит мостом между простыми фундаментальными контейнерами, массивами и связными списками, и более сложными, например, бинарными деревьями, списками пропусков и хеш-таблицами. Эффективный поиск зависит от сложности контейнера, в котором находятся элементы, поэтому мы приводим алгоритмы как для массивов, так и для связных списков. В последующих главах при рассмотрении более сложных контейнеров мы всегда будем говорить об оптимальной стратегии писка для обсуждаемых структур данных.
Само действие поиска элемента в наборе элементов требует возможности отличать элементы друг от друга. Если мы не можем различить два элемента, то не имеет смысла искать один из таких элементов. Таким образом, первая трудность, которую нам потребуется преодолеть, – это сравнение двух элементов, находящихся в одном наборе. Существует два типа сравнения. Первый из них предназначен для несортированных списков элементов, когда все, что нам нужно знать, так это равны ли два элемента. Второй тип используется в отсортированных списках элементов, когда можно добиться повышения эффективности поиска, если имеется возможность определить отношение одного элемента к другому (меньше, равен или больше). (Фактически, операция сравнения определяет, в каком порядке элементы находятся в списке. При поиске в отсортированном списке необходимо выполнять то же самое сравнение, на основе которого был построен список.)
Очевидно, что если элементы принадлежат к целочисленному типу, операция сравнения не представляет никаких трудностей: все мы можем взять два целых числа и определить, отличаются они или нет. В случае строк сравнение усложняется. Можно выполнять сравнение, чувствительное к регистру (т.е. строчные символы будут отличаться от прописных), и сравнение, нечувствительное к регистру (т.е. строчные символы не будут отличаться от прописных), сравнение по локальным таблицам символов (сравнение на основе алгоритмов, специфических для определенной страны или языка) и т.д. Тип set в Delphi, несмотря на то, что он позволяет сравнивать два набора, все же не имеет четко определенного способа определения того, что один набор больше другого (фактически выражение "один набор больше другого" не имеет смысла, если речь не идет о количестве элементов). А что касается объектов, то здесь даже нет метода, который бы позволил сказать, что объект A равен или не равен объекту B (за исключением сравнения указателей на объекты).
Лучше всего на данном этапе рассматривать процедуру сравнения в виде "черного ящика" – функции с четко определенным интерфейсом или синтаксисом, которая в качестве входного параметра принимает два элемента и возвращает результат сравнения – первый элемент меньше второго, первый элемент равен второму или первый элемент больше второго. Для тех типов элементов, которые не имеют определенного порядка (т.е. даже если известно, что два элемента не равны, мы не можем определить, меньше элемент A элемента B или больше), нужно предусмотреть, чтобы функция сравнения возвращала значение, которое трактуется как "не равно".
В книге все функции сравнения принадлежат к типу TtdCompareFunc (этот тип объявлен в файле TDBasics.pas, который можно найти на Web-сайте издательства, в разделе материалов; там же находятся и примеры функций сравнения):
type TtdCompareFunc = function(aData1, aData2 : pointer) : integer; |
Другими словами, функция сравнения в качестве входных параметров принимает два указателя и возвращает целочисленное значение. Возвращаемое значение будет равно 0, если два сравниваемых элемента равны, меньше нуля, если первый элемент меньше второго, и больше нуля, если первый элемент больше второго. Тип параметров aData1 и aData2 определяет сама функция, и она же решает, что делать с переданными данными: привести к определенному классу или просто к типу, который не является указателем.
Приведем пример функции сравнения, которая предполагает, что входные параметры принадлежат к типу longint, а не представляют собой указатели. (Будем считать, что значение sizeof(longint) равно sizeof(pointer). На сегодняшний день это справедливо для всех версий Delphi.)
function TDCompareLongint(aData1, aData2 : pointer) : integer; var L1 : longint absolute aData1; L2 : longint absolute aData2; begin if (L1 < L2) then Result := -1 else if (L1 = L2) then Result := 0 else Result := 1 end; |
Перед тем как в ужасе сказать, что вы бы никогда не вызвали такую функцию сравнения двух значений типа longint, обратите внимание, что этого и не требуется. Приведенная функция предназначена для использования структурами данных, которые принимают элементы в виде указателей (например, список TtdSingleLinkList или стандартный массив TList), и подпрограммами, которые используют такие структуры данных. Если вы разрабатываете функцию поиска, исходя из главных принципов, имеет смысл написать и процедуру сравнения. Остается надеяться, что все мы сможем написать функцию для сравнения двух целых чисел.
Давайте рассмотрим пример функции TDCompareNullStr, предназначенной для сравнения двух строк, завершающихся нулем, не привязываясь к алфавиту определенной страны:
function TDCompareNullStr(aData1, aData2 : pointer) : integer; begin Result := StrComp(PAnsiChar(aData1), PAnsiChar(aData2)); end; |
(В Delphi 1 в модуле TDBasics объявлено, что тип PAnsiChar соответствует типу PChar.) К счастью, для данного примера стандартная функция StrComp возвращает значение того же типа, что и требуется для нашей функции сравнения.
В качестве последнего примера приведем функцию TDCompareNullStrANSI, предназначенную для сравнения двух строк, завершающихся нулем, с учетом локальных таблиц символов:
function TDCompareNullStrANSI(aData1, aData2 : pointer) : integer; begin {$IFDEF Delphi1} Result := lstrcmp(PAnsiChar(aData1), PAnsiChar(aData2)); {$ENDIF} {$IFDEF Delphi2Plus} Result := CompareString(LOCALE_USER_DEFAULT, 0, PAnsiChar(aData1), -1, PAnsiChar(aData2), -1) - 2; {$ENDIF} {$IFDEF Kylix1Plus} Result := strcoll(PAnsiChar(aData1), PAnsiChar(aData2)); {$ENDIF} end; |
В приведенной функции для Delphi 1 и 32-разрядных версий Delphi используются разные коды. Кроме того, обратите внимание, что функция lstrcmp возвращает значения в том виде, который нужен нам. К сожалению, функция CompareString этого не делает. Она возвращает 1, если первая строка меньше второй, 2, если строки равны, и 3, если первая строка больше второй. Поэтому для получения требуемого значения необходимо просто вычесть 2 из результата, возвращаемого функцией CompareString. В Kylix для сравнения строк нужно воспользоваться функцией strcoll из модуля Libc.
Теперь, когда мы определились с функцией сравнения, можно перейти к рассмотрению алгоритмов поиска элемента в массивах и связных списках.
Массивы представляют собой простейшую реализацию набора элементов, для которой можно использовать алгоритм последовательного поиска. Возможны два случая: первый – элементы массива расположены в произвольном порядке и второй – элементы отсортированы. Сначала рассмотрим случай несортированного массива.
Если массив не отсортирован, для поиска определенного элемента может использоваться только один единственный алгоритм: выбирать каждый элемент массива и сравнивать его с искомым. Как правило, такой алгоритм реализуется с помощью цикла For. В качестве примера давайте выполним поиск значения 42 в массиве из 100 целых чисел:
var MyArray : array[0..99] of integer; Inx : integer; begin for Inx := 0 to 99 do if MyArray[Inx] = 42 then Break; if (Inx = 100) then .. значение 42 не было найдено .. else .. значение 42 было найдено в элементе с индексом Inx .. |
Довольно просто, не правда ли? Код выполняет цикл по всем элементам массива, начиная с первого и заканчивая последним, используя Break для выхода из цикла при обнаружении первого элемента, значение которого равно искомому 42. (Оператор Break очень удобно использовать, здесь он ничем не отличается от оператора goto.) После цикла, для того чтобы определить, найден ли элемент, проверяется значение счетчика цикла Inx.
Интересно, сколько читателей в приведенном выше коде нашли ошибку? Проблема заключается в том, что в языке Object Pascal при успешном завершении цикла значение переменной цикла будет не определено. С другой стороны, в случае преждевременного завершения цикла, скажем, с помощью оператора Break, значение переменной цикла будет определено.
В коде предполагается, что перемененная цикла Inx после завершения цикла будет на 1 больше конечного значения для цикла For, даже если цикл будет выполнен успешно. Оказывается, что в 32-разрядных компиляторах (в версиях Delphi от 2 до 7) ошибки не возникает: значение переменной цикла после завершения цикла будет на 1 больше, чем при последнем выполнении цикла. В Delphi 1 код будет работать неправильно: после завершения выполнения цикла переменная цикла будет содержать значение, равное своему значению при последнем выполнении цикла (в нашем примере Inx после полного выполнения цикла будет содержать 99). Кто знает, что будет в следующих версиях Delphi? Вполне возможно, что в будущих версиях Delphi будет изменен оптимизатор компилятора, и переменная цикла после завершения цикла будет получать другое значение. В конце концов, разработчики, описав поведение переменной цикла, оставили за собой право изменения ее значения после выхода из цикла.
Тогда каким образом можно реализовать алгоритм последовательного поиска? Цикл For можно использовать (это самый быстрый метод организации последовательного поиска), однако потребуется ввести флаг, который будет указывать, найден ли искомый элемент. Код несколько усложнится, но зато становится корректным с точки зрения языка программирования:
var MyArray : array[0..99] of integer; Inx : integer; FoundIt : boolean; begin FoundIt := false; for Inx := 0 to 99 do if MyArray[Inx] = 42 then begin FoundIt := true; Break; end; if not FoundIt then .. значение 42 не было найдено .. else .. значение 42 было найдено в элементе с индексом Inx .. |
А теперь рассмотрим функцию поиска элемента в массиве TList с помощью функции сравнения (ее реализацию можно найти в файле TDTList.pas на Web-сайте издательства, в разделе сопровождающих материалов). Если искомый элемент не найден, функция возвращает -1, в противном случае возвращается индекс элемента.
function TDTListIndexOf(aList : TList; aItem : pointer; aCompare : TtdCompareFunc) : integer; var Inx : integer; begin for Inx := 0 to pred(aList.Count) do if (aCompare(aList.List^[Inx], aItem) = 0) then begin Result := Inx; Exit; end; {если мы попали сюда, значит искомый элемент не найден} Result := -1; end; |
Эта функция работает не так как метод TList.IndexOf, который предназначен для поиска элемента в массиве путем сравнения значений указателей. Фактически он в своем внутреннем списке указателей осуществляет поиск элемента как указателя. С другой стороны, функция TDTListIndexOf осуществляет поиск самого элемента, вызывая для сравнения искомого и текущего элемента функцию сравнения. Функция сравнения может сравнивать просто значения указателей или преобразовывать указатели во что-нибудь более значимое, например, в класс или запись, а затем сравнивать поля.
Обратите внимание, что в реализации функции с целью повышения эффективности применяется небольшая хитрость. Вместо сравнения aItem с aList[Inx] выполняется сравнение с aList.List^[Inx]. Зачем? Компилятор преобразовывает первое сравнение в вызов функции, а затем вызываемая функция, TList.Get, перед возвратом указателя из внутреннего массива указателей проверяет переданный ей индекс на предмет попадания в диапазон от 0 до количества элементов (вызывая исключение, если условие не соблюдается). Но мы знаем, что индекс находится в требуемом диапазоне, поскольку используется цикл от 0 до количества элементов минус 1. Поэтому нам не нужно считывать значение свойства Items и вызывать метод TList.Get. Можно получить доступ непосредственно к массиву указателей (свойство List экземпляра TList).
Эта хитрость (использование свойства List экземпляра TList) вполне корректна. Если вы уверены, что значения индекса не выходят за пределы допустимого диапазона, можно исключить проверку на предмет попадания в диапазон за счет непосредственного доступа к массиву List, а не с помощью свойства Items. Тем не менее, ее применение при итерации по массиву TList или в коде, который может привести к выходу индекса за пределы допустимого диапазона, не желательно. Лучше обезопасить себя, нежели потом сожалеть. |
В классе TtdRecordList (который описан в главе 2) для организации последовательного поиска можно пользоваться методом IndexOf (см. листинг 4.6).
function TtdRecordList.IndexOf(aItem : pointer; aCompare : TtdCompareFunc) : integer; var ElementPtr : PAnsiChar; i : integer; begin ElementPtr := FArray; for i := 0 to pred(Count) do begin if (aCompare(aItem, ElementPtr) = 0) then begin Result := i; Exit; end; inc(ElementPtr, FElementSize); end; Result := -1; end; |
Как видите, время выполнения алгоритма последовательного поиска напрямую зависит от количества элементов в массиве. В лучшем случае мы можем найти требуемый элемент с первой попытки (если он будет первым в массиве), но вполне вероятно, что мы обнаружим его в самом конце, после просмотра всех элементов. В среднем для массива размером n для обнаружения искомого элемента придется пройти n/2 элементов. В любом случае, если искомого элемента нет в массиве, будут просмотрены все n элементов. Таким образом, операция последовательного поиска принадлежит к классу O(n).
А что можно сказать о сортированном массиве? Первое, что следует отметить, – простой алгоритм последовательного поиска в отсортированном массиве будет работать ничуть не хуже (или не лучше, в зависимости от вашей точки зрения), чем в несортированном. Операция поиска будет принадлежать к классу O(n).
Тем не менее, алгоритм поиска можно улучшить. Если искомого элемента нет в массиве, поиск можно выполнить намного быстрее. Фактически мы выполняем итерации по массиву, как и раньше, но теперь только до тех пор, пока не будет найден элемент, больший или равный искомому. Если обнаружен элемент, равный искомому, поиск завершается успешно. Если же обнаружен элемент больше искомого, значит, искомый элемент в массиве отсутствует, поскольку массив отсортирован, а мы дошли до элемента большего, чем искомый. Все последующие элементы также будут больше искомого. Следовательно, поиск можно прекратить.
function TDTListSortedIndexOf(aList : TList; aItem : pointer; aCompare : TtdCompareFunc) : integer; var Inx, CompareResult : integer; begin {искать первый элемент больший или равный элементу aItem} for Inx := 0 to pred(aList.Count) do begin CompareResult := aCompare(aList.List^[Inx], aItem); if (CompareResult >= 0) then begin if (CompareResult = 0) then Result := Inx else Result := -1; Exit; end; end; {если мы попали сюда, значит искомый элемент не найден} Result := -1; end; |
Обратите внимание, что функция сравнения вызывается только один раз при каждом выполнении цикла. Мы не знаем, что делает функция aCompare – для нас это "черный ящик". Следовательно, желательно ее вызывать как можно реже. Поэтому при каждом выполнении цикла мы вызываем ее только один раз и сохраняем полученный результат в переменной целого типа. После этого переменную можно использовать сколько угодно раз, не вызывая функцию.
Как уже говорилось, приведенная функция поиска нисколько не увеличивает скорость обнаружения искомого элемента, если искомый элемент присутствует в массиве (в среднем, как и ранее, для этого потребуется провести n/2 сравнений). Единственным ее преимуществом перед предыдущей функцией является то, что при отсутствии искомого элемента в массиве результат будет получен быстрее. Скоро мы рассмотрим алгоритм бинарного поиска, который позволит повысить быстродействие в обоих случаях.
В связных списках последовательный поиск выполняется точно так же, как и в массивах. Тем не менее, элементы проходятся не по индексу, а по указателю Next. Для класса TtdSingleLinkList, описанного в главе 3, можно разработать две следующих функции: первая – для выполнения поиска по несортированному связному списку, и вторая – по отсортированному. Функции просто указывают, найден ли искомый элемент. В случае, если элемент найден, список будет установлен в позицию искомого элемента. В функции для отсортированного списка курсор будет установлен в позицию, где должен находиться искомый элемент, чтобы список оставался отсортированным.
function TDSLLSearch(aList : TtdSingleLinkList; aItem : pointer; aCompare : TtdCompareFunc) : boolean; begin with aList do begin MoveBeforeFirst; MoveNext; while not IsAfterLast do begin if (aCompare(Examine, aItem) = 0) then begin Result := true; Exit; end; MoveNext; end; end; Result := false; end; function TDSLLSortedSearch(aList : TtdSingleLinkList; aItem : pointer; aCompare : TtdCompareFunc) : boolean; var CompareResult : integer; begin with aList do begin MoveBeforeFirst; MoveNext; while not IsAfterLast do begin CompareResult := aCompare(Examine, aItem); if (CompareResult >= 0) then begin Result := (CompareResult = 0); Exit; end; MoveNext; end; end; Result := false; end; |
Соответствующие функции для класса TtdDoubleLinkList будут точно такими же.
В случае отсортированного списка можно использовать более эффективный алгоритм бинарного поиска. Сначала рассмотрим его на примере массива, а затем покажем, как его изменить для связных списков.
Алгоритм бинарного поиска применим только для отсортированных контейнеров.
Предположим, что у нас имеется отсортированный массив. Как было показано ранее, алгоритм последовательного поиска даже при использовании выхода из цикла в случае отсутствия в списке искомого элемента принадлежит к классу O(n). Каким образом можно улучшить быстродействие?
Ответом может служить бинарный поиск. Он основан на стратегии "разделяй и властвуй": начинаем с большой проблемы, разбиваем ее на маленькие проблемы, которые легче решить, а, затем, следовательно, решаем всю большую проблему.
Бинарный поиск работает следующим образом. Берем средний элемент массива. Равен ли он искомому элементу? Если да, то поиск успешно завершен. В противном случае, если искомый элемент меньше среднего, то можно сказать, что, если элемент присутствует в массиве, он находится в первой половине. С другой стороны, если искомый элемент больше среднего, он должен находиться во второй половине. Таким образом, одним сравнением мы разбили нашу проблему на две части. Теперь мы применяем тот же алгоритм к выбранной части массива: находим средний элемент и определяем, в какой половине (точнее уже в четвертой части) находится искомый элемент. Мы снова делим проблему на две части. Описанные операции продолжаются до тех пор, пока искомый элемент не будет найден (разумеется, если он присутствует в массиве).
Это и есть алгоритм бинарного поиска. Поскольку размер массива при каждом выполнении цикла уменьшается в два раза, быстродействие алгоритма будет выражаться как O(log(n)), т.е. скорость работы алгоритма примерно пропорциональна функции двоичного логарифма log2 от количества элементов в массиве (таким образом, возведение количества элементов массива во вторую степень приведет к увеличению времени поиска только в два раза).
Ниже приведен пример выполнения бинарного поиска в массиве TList (функцию можно найти в файле TDTList.pas на Web-сайте издательства, в разделе сопровождающих материалов).
function TDTListSortedIndexOf(aList : TList; aItem : pointer; aCompare : TtdCompareFunc) : integer; var L, R, M : integer; CompareResult : integer; begin {задать значения для индексов первого и последнего элементов} L := 0; R := pred(aList.Count); while (L <= R) do begin {вычислить индекс среднего элемента} M := (L + R) div 2; {сравнить значение среднего элемента с искомым значением} CompareResult := aCompare(aList.List^[M], aItem); {если значение среднего элемента меньше искомого значения, переместить левый индекс на позицию до среднего индекса} if (CompareResult < 0) then L := succ(M) {если значение среднего элемента больше искомого значения, переместить правый индекс на позицию после среднего индекса} else if (CompareResult > 0) then R := pred(M) {в противном случае искомый элемент найден} else begin Result := M; Exit; end; end; Result := -1; end; |
Для описания подмассива, рассматриваемого в текущий момент, используются две переменных – L и R, которые хранят, соответственно, левый и правый индексы. Первоначально значения этих переменных устанавливаются равными 0 (первый элемент массива) и Count-1 (последний элемент массива). Затем мы входим в цикл While, из которого выйдем после обнаружения в массиве искомого элемента или когда значение переменной L превысит значение переменной R, что означает, что искомый элемент в массиве отсутствует. При каждом выполнении цикла вычисляется индекс среднего элемента (фактически это среднее значение между L и R). Затем значение элемента со средним индексом сравнивается с искомым значением. Если значение среднего элемента меньше, чем искомое, мы переносим левый индекс на позицию после среднего. В противном случае мы переносим правый индекс на позицию перед средним. Таким образом, мы определяем новый подмассив для поиска. Если же значение среднего элемента равно искомому, поиск завершен.
Для примера на рис. 4.1 приведены шаги, выполняемые при бинарном поиске буквы d в отсортированном массиве, содержащем буквы от a до k. На шаге (а) переменная L указывает на первый элемент (индекс 0), а R – на последний (индекс 10). Это означает, что значение переменной M будет составлять 5. Далее мы выполняем сравнение: значение элемента с индексом 5 равно f, а это больше искомого значения d.
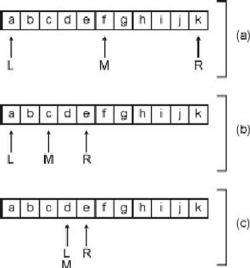
Рисунок 4.1. Бинарный поиск в массиве
Согласно алгоритму, мы устанавливаем значение R равным M-1 (таким образом, правая граница подмассива теперь находится слева от среднего элемента). Это означает, что значение R теперь равно 4. Новое значение среднего индекса будет равно 2, как показано на шаге (b). Выполняем сравнение: буква c (значение элемента с индексом 2) меньше, чем d.
Теперь, в соответствии с алгоритмом, необходимо установить индекс L за индексом M (т.е. M+1 или 3). Новое значение переменной M на шаге (с) равно 3. Выполняем сравнение: элемент с индексом 3 содержит букву d, а это и есть наше искомое значение. Поиск завершен.
Изучая код листинга 4.9, можно придти к выводу, что маловероятно, чтобы бинарный поиск использовался для связных списков, если, конечно, не воспользоваться индексным доступом к элементам списка, который, как уже упоминалось в главе 3, приводит к снижению быстродействия.
Но, тем не менее, реализация бинарного поиска для связных списков оказывается не такой уж и неразрешимой проблемой. Во-первых, нужно понимать, что в общем случае переход по ссылке выполняется гораздо быстрее, нежели вызов функции сравнения. Следовательно, можно сказать, что переход по ссылке – это "хорошо", а вызов функции сравнения – "плохо". Это означает, что следует стремиться к минимизации вызовов функции сравнения. (Поскольку для нас функция сравнения – "черный ящик", мы не можем сказать, сколько времени требуется на ее выполнение: много или мало, по крайней мере, по сравнению со временем, требуемым на переход по ссылке.) Во-вторых, необходимо иметь доступ к "внутренностям" связного списка.
Давайте рассмотрим принцип организации бинарного поиска на примере обобщенного связного списка, а затем рассмотрим код для классов TtdSingleLinkList и TtdDoubleLinkList. Для нашего обобщенного связного списка должно быть известно количество содержащихся в нем элементов, поскольку оно понадобится при реализации алгоритма бинарного поиска. Кроме того, будем считать, что связный список содержит фиктивный начальный узел.
А теперь сам алгоритм.
Давайте рассмотрим работу этого алгоритма на примере. Предположим, что имеется следующий связный список из пяти узлов, в котором необходимо найти узел B:
Начальный узел ® A ® B ® C ® D ® E ® nil |
На первом шаге переменной BeforeList присваивается значение начального узла, а на втором переменной ListCount присваивается значение 5. Делим ListCount на два, округляем до целого, и присваиваем полученное значение (3) переменной MidPoint (шаг 3). По ссылкам от узла BeforeList отсчитываем три узла: A, B, C (шаг 4). Сравниваем текущий узел с искомым (шаг 5). Его значение больше искомого B, следовательно, устанавливаем значение переменной ListCount равным 2 (шаг 7). Еще раз выполняем цикл. Делим ListCount на два, округляем до целого и получаем 1 (шаг 3). По ссылкам от узла BeforeList отсчитываем один узел: А (шаг 4). Сравниваем значение текущего узла с искомым значением (шаг 5). Оно меньше значения B, следовательно, записываем в BeforeList значение узла B, а переменной ListCount присваиваем значение 1 (шаг 6) и снова выполняем цикл. В этот раз MidPoint получит значение 1 (т.е. значение ListCount, деленное на два и округленное до целого). Переходим по ссылке от узла BeforeList на один шаг и находим искомый узел.
Если вы считаете, что в процессе выполнения алгоритма искомый узел был пройден несколько раз, то вы совершенно правы. Но следует иметь в виду, что вызов функции сравнения может быть намного медленнее, чем переход по ссылкам (например, если элементы списка представляют собой строки длиной 1000 символов, то для определения соотношения между строками функции сравнения придется сравнить в среднем 500 символов). Если бы связный список содержал целые числа, а мы отказались бы от частого использования функции сравнения, то быстрее всех оказался бы алгоритм последовательного поиска.
Ниже приведена функция бинарного поиска для класса TtdSingleLinkList.
function TtdSingleLinkList.SortedFind(aItem : pointer; aCompare : TtdCompareFunc) : boolean; var BLCursor : PslNode; BLCursorIx : longint; WorkCursor : PslNode; WorkParent : PslNode; WorkCursorIx : longint; ListCount : longint; MidPoint : longint; i : integer; CompareResult :integer; begin {подготовительные операции} BLCursor := FHead; BLCursorIx := -1; ListCount := Count; {пока в списке имеются узлы…} while (ListCount <> 0) do begin {вычислить положение средней точки; оно будет не менее 1} MidPoint := (ListCount + 1) div 2; {переместиться вперед до средней точки} WorkCursor := BLCursor; WorkCursorIx := BLCursorIx; for i := 1 to MidPoint do begin WorkParent := WorkCursor; WorkCursor := WorkCursor^.slnNext; inc(WorkCursorIx); end; {сравнить значение узла с искомым значением} CompareResult := aCompare(WorkCursor^.slnData, aItem); {если значение узла меньше искомого, уменьшить размер списка и повторить цикл} if (CompareResult < 0) then begin dec(ListCount, MidPoint); BLCursor := WorkCursor; BLCursorIx := WorkCursorIx; end {если значение узла больше искомого, уменьшить размер списка и повторить цикл} else if (CompareResult > 0) then begin ListCount := MidPoint - 1; end {в противном случае искомое значение найдено; установить реальный курсор на найденный узел} else begin FCursor := WorkCursor; FParent := WorkParent; FCursorIx := WorkCursorIx; Result := true; Exit; end; end; Result := false; end; |
Функция бинарного поиска для класса TtdDoubleLinkList аналогична приведенной функции.
Если необходимо создать отсортированный массив или связный список, у нас существует выбор того или иного метода поддержания порядка элементов. Можно сначала вставлять элементы в контейнер, а затем их сортировать и сортировать содержимое контейнера при вставке каждого нового элемента, или же при выполнении вставки находить позицию, вставив новый элемент в которую контейнер останется отсортированным. Если предполагается, что контейнер будет часто использоваться в отсортированном виде, тогда имеет смысл при вставке сохранять правильный порядок элементов.
В таком случае наша задача сводится к вычислению положения нового элемента в отсортированном списке. После определения позиции мы просто вставляем в нее новый элемент. Ранее говорилось, что последовательный поиск может помочь определить точку вставки, но, к сожалению, быстродействие последовательного поиска достаточно низкое. Можно ли для определения точки вставки воспользоваться бинарным поиском?
Оказывается, можно. Посмотрите внимательно на реализацию бинарного поиска для массива, приведенную в листинге 4.9. Когда выполнение цикла завершается, и искомый элемент не найден, что можно определить на основании значений переменных L, R и M? Во-первых, очевидно, что L>R. Рассмотрим, что происходит при выполнении цикла в последний раз. В начале цикла мы должны были иметь L=R или L=R-1. При этом вычисление даст, что M=L. Если бы разница между L и R была больше, скажем, L=R-2, тогда значение M попало бы в диапазон между L и R, и цикл был бы выполнен, по крайней мере, еще один раз.
Если при выполнении цикла в последний раз искомый элемент был меньше, чем элемент в позиции M, то переменная R получила бы значение M-1, и цикл завершился бы. Мы уже знаем, что искомого значения не было до элемента M, поэтому можно сделать вывод, что новый элемент должен быть вставлен между элементами M-1 и M. Другими словами, мы вставляем элемент в позицию M.
С другой стороны, если бы искомый элемент был больше элемента в позиции M, то переменная L получила бы значение M+1. В этом случае можно принять, что в начале цикла L=R. В противном случае цикл был бы выполнен еще один раз. Мы уже знаем, что искомого значения не было после элемента M, поэтому можно сделать вывод, что новый элемент должен быть вставлен между элементами M и M+1. Другими словами, мы вставляем элемент в позицию M+1.
Таким образом, новый элемент должен вставляться в позицию M или M+1 в зависимости от того, что произошло при последнем выполнении цикла. Но давайте подумаем еще раз. Разве между описанными двумя случаями нет ничего общего? Оказывается, что на место вставки в обоих случаях указывает значение переменной L. Таким образом, вставка выполняется в позицию L.
В приведенном ниже листинге показано, каким образом можно вставить новый элемент в массив TList. В коде предполагается, что если вновь вставляемый элемент уже присутствует в массиве, вставка будет игнорироваться (другими словами, повторение элементов не допускается). Функция возвращает индекс вставленного элемента. Легко проверить, что приведенная функция будет работать даже в случае, когда список перед вставкой пуст.
function TDTListSortedInsert(aList : TList; aItem : pointer; aCompare : TtdCompareFunc) : integer; var L, R, M : integer; CompareResult : integer; begin {задать значения левого и правого индексов} L := 0; R := pred(aList.Count); while (L <= R) do begin {вычислить индекс среднего элемента} M := (L + R) div 2; {сравнить значение среднего элемента с заданным значением} CompareResult := aCompare(aList.List^[M], aItem); {если значение среднего элемента меньше заданного значения, переместить левый индекс на позицию после среднего элемента} if (CompareResult < 0) then L := succ(M) {если значение среднего элемента больше заданного значения, переместить правый индекс на позицию перед средним элементом} else if (CompareResult > 0) then R := pred(M) {в противном случае элемент найден, выйти из функции} else begin Result := M; Exit; end; end; Result := L; aList.Insert(L, aItem); end; |
Для связного списка функция будет еще проще, поскольку нам не нужно решать, каким образом вычислять индекс для вставки нового элемента. Поиск сам указывает на точку вставки элемента.
Эта глава была посвящена поиску. Было показано, каким образом выполняется последовательный поиск и как можно улучшить алгоритм поиска для отсортированных массивов и связных списков. Было доказано, что для отсортированных контейнеров гораздо быстрее будет алгоритм бинарного поиска. И, наконец, мы рассмотрели использование алгоритма бинарного поиска для вставки нового элемента в требуемое место отсортированного массива.
 Оценка 15 Оценка 15   Оценить Оценить       
|