Сообщений 0    Оценка 50 [+0/-1]         Оценить

Метод воксельной растеризации и обработки

Автор: Арсланов Дмитрий Мерзагитович

Опубликовано: 17.02.2012
Исправлено: 10.12.2016
Версия текста: 1.1

Введение

Одной из основных задач компьютерного моделирования является получение модели объекта предметной области в виде упорядоченной совокупности векторных элементов и процесс ее интерактивной обработки. Частным случаем такой обработки является визуализация, под которой понимается процесс конвертации векторной модели в растровое изображение (пиксельное или точечное) для представления пользователю, т.е. вывода на экран или принтер, или для сохранения в файле. Методы визуализации можно разделить на две группы по порядку следования операций при получении растрового изображения: от пикселей изображения к элементам векторной модели – методы бросания лучей и его производные; и от элементов векторной модели к пикселям изображения – растеризация [1].

Сегодня становится возможным ускорять методы бросания лучей применением вычислений общего назначения на графическом процессоре (GPGPU) [2, 5]. Однако на практике растеризация, тем не менее, остается быстрее методов бросания лучей. В отличие от методов бросания лучей растеризация не позволяет непосредственно получить фотореалистичные растровые изображения. Но программируемый шейдерный конвейер современных графических процессоров позволяет реализовать сложные методы визуализации, основанные на растеризации. Поэтому возможно имитировать те или иные эффекты при помощи специальных приемов [1, 4, 7].

Триангуляционные модели благодаря своей структуре наиболее эффективны при растеризации и бросании лучей. Именно они и применяются для создания интерактивных приложений компьютерной графики и фотореалистичной визуализации [1]. Но подобная структура моделей объектов неэффективна для задач, где обработка данных шире и сложнее задач визуализации. При более сложной обработке триангуляционная модель требует реализации и более сложных методов для получения желаемого результата. Примерами такой обработки могут служить генерация конструктивной объемной геометрии, образованной, например, в результате операций объединения, пересечения или разности объемных примитивов, таких как шар, куб или конус; моделирование физических процессов, протекающих в веществе, например, потоки жидкости или газа; движение и взаимодействие частиц или тел; генерация комплексных поверхностей и внутреннего строения объектов; деформация, разрушения и т.п. Например, для реализации высокоуровневой операции построения триангуляционной модели тела, представляющего собой разность триангуляционных моделей куба и шара, потребуется нахождение линий пересечений треугольников куба и шара и корректная генерация нового множества индексов для полученного множества вершин, что является достаточно сложной задачей [9].

В отличие от триангуляционных моделей, воксельные модели предлагают более простой и эффективный способ обработки данных. На рисунке 1 приведен результат растеризации воксельной модели рассмотренного объекта. Опишем метод, при помощи которого можно получить данное изображение.

Рисунок 1. Результат растеризации воксельной модели тела, представляющего собой разность куба и шара.

Воксельная модель

Для начала дадим определение воксельной модели, которая будет использоваться в рамках данной работы. Оно будет опираться на теорию алгебраических систем [13]. Подобное определение хорошо согласуется с представлением объектов классов и структур типов данных в языках программирования. При определении введем особое обозначение для векторов-строк и их элементов. Например, вектор-строка из трех элементов запишется как кортеж

x = {x[0], x[1], x[2]} = {x[i]}.

Такое описание удобно для математических выражений и соответствует виду, используемому для работы с элементами массивов в языках программирования. Здесь и далее будет использоваться i = 0, 1, 2.

Введем множество D действительных чисел в единичном интервале:

D = [0; 1],

которое будем рассматривать как основную область определения и область значений вводимых функций.

Рассмотрим подмножество f декартового произведения пяти множеств D:

D⁵ = D  D  D  D  D,

f  D⁵.

Элементы f представляют собой упорядоченные последовательности чисел (x[0], x[1], x[2], t, f) или (x, t, f). Для них справедливо следующее условие: для любых четырех элементов из области определения существует единственный элемент из области значения, такой, что их упорядоченная последовательность является элементом введенного подмножества, – что можно записать в виде:

 x[i]  D, t  D, f D: (x, t, f) f,

f = {(x, t, f)}.

f представляет собой динамическое, т.е. меняющееся с течением времени, пространственное скалярное поле, которое будем полагать заданным в левой локальной прямоугольной трехмерной системе координат OUVW, где введем вектор-строку длин единичных отрезков вдоль соответствующих осей

x ₀ = {x₀[i]},

и вектор-строку размеров области определения вдоль осей в соответствующих единичных отрезках

D = {D[i]},

элементы которого найдутся как

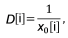
а также вектор-строку целочисленных координат точки в пространстве области определения

d = {d[i]},

элементы которого принимают значения

d[i] = 0, 1, …, (D[i] - 1).

Изменение значений скалярного поля будем рассматривать только в точках, кратных

x[i] = d[i]x₀[i].

Будем полагать, что значения скалярного поля могут быть равны только значениям

f = vf₀,

где дискрета значений скалярного поля

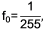
а целочисленные значения скалярного поля

v = 0, 1, …, 255,

в рамках данной работы будем называть вокселями.

Значения скалярного поля будем рассматривать в моменты времени t, следующие друг за другом с периодом t_min. За условный промежуток времени D будет рассмотрено

состояний модели. Каждое новое рассматриваемое состояние будем называть кадром или тактом обработки. Его индекс пробегает значения

s = 0, 1, …, (S - 1).

В результате введенное скалярное поле является дискретным. Будем использовать следующие эквивалентные обозначения его функционального отношения или отображения D⁴D:

f(x[0], x[1], x[2], t) = f(x, t) = f[d[0], d[1], d[2], s] = f[d, s],

Данное скалярное поле и будем называть воксельной моделью. Отметим некоторые особенности такого определения воксельной модели.

Во-первых, размер вокселя модели составляет один байт, что является оптимальным выбором для большинства задач, так как с одной стороны позволяет сопоставить с вокселями достаточный ряд параметров, а с другой экономно расходовать память.

Во-вторых, данный вид модели ориентирован, прежде всего, на интерактивную обработку и визуализацию. t_min будем рассматривать как выраженный в условных единицах минимально возможный интервал времени, который может пройти между сменой состояний воксельной модели в программе, т.е. между кадрами визуализации или тактами обработки модели. Если t_min не превышает максимально возможный интервал времени t_max между сменой состояний воксельной модели, также выраженный в условных единицах, тогда обработка и визуализация воксельной модели считается интерактивной:

t_min ≤ t_max.

Для различных задач допускается варьирование t_max в пересчете из условных единиц от нескольких миллисекунд до нескольких минут. Масштаб реального времени задачи зависит от того, за какое максимально допустимое время требуется перебрать все состояния модели.

В-третьих, будем полагать, что в общем случае состояние s воксельной модели заранее не известно и формируется в ходе обработки на очередном такте перед визуализацией. По этой причине не используются специальные оптимизирующие структуры данных. Примером таких структур могут служить разряженные воксельные октодеревья, популярные при визуализации заранее определенных воксельных моделей. В частности, они позволяют определить требуемый уровень детализации при визуализации [2]. Их построение потребуется для каждого такта обработки в случае использования, что будет неэффективно, так как подобные высокие затраты вычислительных ресурсов на построение дают выигрыш только при повторном использовании, и производительность решения будет снижена настолько, что оно может потерять требуемый уровень интерактивности.

Обработка

Опираясь на введенное определение, построим воксельную модель рассматриваемого тела, представляющего собой разность куба и шара, представленного на рисунке 1. Для этого для дискретных точек x в пределах области определения скалярного поля введем функции куба и эллипсоида. Значения функций внутри куба и эллипсоида будут равны v, а за пределами 1 - v. Границы куба будут задаваться координатами его минимальной точки m = {x_min, y_min, z_min} и максимальной точки M = {x_max, y_max, z_max}. Эллипсоид будет задаваться центром c = {c_x, c_y, c_z} и радиусами r = {r_x, r_y, r_z} вдоль соответствующих осей.

Функцию куба представим в виде

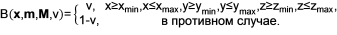
Функцию эллипсоида запишем как

где

x_min = c_x - r_x,

x_max = c_x + r_x,

y_min = c_y – r_y,

y_max = c_y + r_y,

z_min = c_z – s,

z_max = c_z + s,

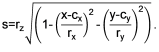
Предполагая, что форма тела не меняется с течением времени, запишем искомую воксельную модель как

f(x, t) = B(x, m, M, 1)E(x, c, r, 0).

Как видно из этого примера, поэлементное умножение матриц для воксельной модели проще методов триангуляции. Приведем реализацию рассмотренного примера на C# и HLSL.

      float3 Dim0;
float3 Dim1;
float Voxel;
uint Stage;
RWTexture3D<float4> VolumeUAV;

[numthreads(1, 1, 1)]
void Box(uint3 threadId : SV_DispatchThreadID)
{
    float3 position = float3(threadId.x, threadId.y, Stage);
    if (position.x >= Dim0.x && position.x <= Dim1.x &&
        position.y >= Dim0.y && position.y <= Dim1.y &&
        position.z >= Dim0.z && position.z <= Dim1.z)
    {
        VolumeUAV[position] = float4(0.0f, 0.0f, 0.0f, Voxel);
    }
}

[numthreads(1, 1, 1)]
void Ellipsoide(uint3 threadId : SV_DispatchThreadID)
{
    float3 position = float3(threadId.x, threadId.y, Stage);
    float s = sqrt(pow(Dim1.z, 2.0f) * (1.0f - pow((position.x - Dim0.x) / Dim1.x, 2.0f) - pow((position.y - Dim0.y) / Dim1.y, 2.0f)));
    float3 Min = float3(Dim0.x - Dim1.x, Dim0.y - Dim1.y, Dim0.z - s);
    float3 Max = float3(Dim0.x + Dim1.x, Dim0.y + Dim1.y, Dim0.z + s);
    if (position.x >= Min.x && position.x <= Max.x &&
        position.y >= Min.y && position.y <= Max.y &&
        position.z >= Min.z && position.z <= Max.z)
    {
        VolumeUAV[position] = float4(0.0f, 0.0f, 0.0f, Voxel);
    }
}

technique11 VoxelProcess
{
    pass BuildBox
    {
        SetBlendState(BlendingDisable, float4(0.0f, 0.0f, 0.0f, 0.0f), 0xFFFFFFFF);
        SetDepthStencilState(DepthTestDisable, 0);
        SetRasterizerState(NoneCulling);
        SetRenderTargets(NULL, NULL);
        SetVertexShader(NULL);
        SetHullShader(NULL);
        SetDomainShader(NULL);
        SetGeometryShader(NULL);
        SetPixelShader(NULL);
        SetComputeShader(CompileShader(cs_5_0, Box()));
    }
    pass BuildEllipsoide
    {
        SetBlendState(BlendingDisable, float4(0.0f, 0.0f, 0.0f, 0.0f), 0xFFFFFFFF);
        SetDepthStencilState(DepthTestDisable, 0);
        SetRasterizerState(NoneCulling);
        SetRenderTargets(NULL, NULL);
        SetVertexShader(NULL);
        SetHullShader(NULL);
        SetDomainShader(NULL);
        SetGeometryShader(NULL);
        SetPixelShader(NULL);
        SetComputeShader(CompileShader(cs_5_0, Ellipsoide()));
    }
}

      using SlimDX;
using SlimDX.Direct3D11;
using SlimDX.DXGI;

namespace VoxelSample
{
    public partial class Volume
    {
        Texture3D voxels;
        ShaderResourceView voxelSRV;
        UnorderedAccessView voxelUAV;

        public Vector3 Size { get; private set; }

        Texture3DDescription VoxelDescription
        {
            get
            {
                return new Texture3DDescription()
                {
                    BindFlags = BindFlags.ShaderResource | BindFlags.UnorderedAccess,
                    CpuAccessFlags = CpuAccessFlags.None,
                    Depth = (int)Size.X,
                    Format = Format.A8_UNorm,
                    Height = (int)Size.Y,
                    MipLevels = 1,
                    OptionFlags = ResourceOptionFlags.None,
                    Usage = ResourceUsage.Default,
                    Width = (int)Size.Z
                };
            }
        }

        public Volume()
        {
            Size = new Vector3(256);
            voxels = new Texture3D(device, VoxelDescription);
            voxelSRV = new ShaderResourceView(device, voxels);
            voxelUAV = new UnorderedAccessView(device, voxels);
            volume.Box(1.0f, new Vector3(64.0f, 64.0f, 117.0f), new Vector3(192.0f, 192.0f, 245.0f));
            volume.Ellipsoide(0.0f, new Vector3(128.0f, 128.0f, 181.0f), new Vector3(80.0f));
            volume.Box(0.66f, new Vector3(0.0f, 0.0f, 245.0f), new Vector3(255.0f));
            Texture3D.SaveTextureToFile(device.ImmediateContext, voxels, ImageFileFormat.Dds, "sample.dds");
        }

        public void Box(float voxel, Vector3 min, Vector3 max)
        {
            effect.GetVariableByName("Voxel").AsScalar().Set(voxel);
            effect.GetVariableByName("Dim0").AsVector().Set(min);
            effect.GetVariableByName("Dim1").AsVector().Set(max);
            effect.GetVariableByName("VolumeUAV").AsUnorderedAccessView().SetView(voxelUAV);
            for (uint z = 0; z < Size.Z; z++)
            {
                effect.GetVariableByName("Stage").AsScalar().Set(z);
                effect.GetTechniqueByName("VoxelProcess").GetPassByName("BuildBox").Apply(device.ImmediateContext);
                device.ImmediateContext.Dispatch((int)Size.X, (int)Size.Y, 1);
                device.ImmediateContext.Flush();
            }
            effect.GetVariableByName("VolumeUAV").AsUnorderedAccessView().SetView(null);
            effect.GetTechniqueByName("Process").GetPassByName("BuildBox").Apply(device.ImmediateContext);
        }

        public void Ellipsoide(float voxel, Vector3 origin, Vector3 radius)
        {
            effect.GetVariableByName("Voxel").AsScalar().Set(voxel);
            effect.GetVariableByName("Dim0").AsVector().Set(min);
            effect.GetVariableByName("Dim1").AsVector().Set(max);
            effect.GetVariableByName("VolumeUAV").AsUnorderedAccessView().SetView(voxelUAV);
            for (uint z = 0; z < Size.Z; z++)
            {
                effect.GetVariableByName("Stage").AsScalar().Set(z);
                effect.GetTechniqueByName("VoxelProcess").GetPassByName("BuildBox").Apply(device.ImmediateContext);
                device.ImmediateContext.Dispatch((int)Size.X, (int)Size.Y, 1);
                device.ImmediateContext.Flush();
            }
            effect.GetVariableByName("VolumeUAV").AsUnorderedAccessView().SetView(null);
            effect.GetTechniqueByName("Process").GetPassByName("BuildEllipsoide").Apply(device.ImmediateContext);
        }
    }
}

Отметим следующие особенности приведенного кода.

Обработку, связанную с изменениями значений вокселей на каждом такте s, эффективно организовать средствами DirectCompute, т.е. при помощи вычислительных шейдеров Direct3D 10/11. Direct3D позволяет обрабатывать, визуализировать, передавать данные от центрального процессора графическому процессору и обратно с использованием одних и тех же ресурсов (текстур и буферов), что облегчает интеграцию комплексных методов обработки и визуализации [5].

Для представления воксельной модели с целью обработки средствами графического процессора согласно данному определению удобно использовать трехмерную текстуру с размером текселя (вокселя) в один байт. Для центрального процессора в свою очередь может быть использован массив байт. Средствами Direct3D для воксельных моделей в виде трехмерных текстур можно организовать сохранение и загрузку файлов в формате *.dds. Для просмотра этих файлов штатной утилитой DirectX Texture Tool необходимо использовать формат текселя A8_UNorm.

Особенность обработки данных на графическом процессоре заключается в том, что практически для каждого отдельного элемента ресурса может быть запущен отдельный процесс обработки. Так, например, вершинный шейдер выполняется для вершин примитивов, пиксельные шейдеры выполняются для пикселей из области проекции примитива. По сути шейдерная программа представляет собой код для отдельного процесса, обрабатывающего отдельный элемент ресурса. Таким образом, может быть создан большой объем параллельных вычислительных процессов с высокой скоростью выполнения. Следует обратить внимание на то, что идентификация вычислительных шейдеров осуществляется аналогично положению вокселя в предложенной модели. При этом существует возможность запустить необходимый объем вычислительных процессов [8]. Поэтому код вычислительного шейдера обрабатывает отдельный воксель модели.

Для одного и того же ресурса в Direct3D могут быть созданы два вида: вид ресурса шейдера (ShaderResourceView) и вид с неупорядоченным доступом (UnorderedAccessView). Вид ресурса шейдера используется только для чтения как в контексте растеризации в пиксельном шейдере, так и в контексте обработки в вычислительном шейдере. Вид с неупорядоченным доступом, как правило, используется для записи в контексте обработки в вычислительном шейдере. Использование этого вида в том числе и для чтения бывает затруднительным, поскольку за одну операцию при помощи такого вида возможно считывание только одного байта. Для считывания из этого вида элемента, представляющего собой структуру, может потребоваться сложный код, в целом снижающий производительность. Использование двух видов одного ресурса: одного для чтения, другого для записи, – избавляет от подобных проблем, но при этом существует ограничение: в шейдере может быть использован только один вид. Ситуаций, когда в шейдере требуются оба вида, при грамотной организации вычислений возникать не должно. В противном случае требуется синхронизация операций, что проще всего организуется разбиением обработки на проходы разными шейдерами, где вид ресурса может быть переключен. При использовании двух видов одного ресурса нужно внимательно следить за привязкой видов ресурса к различным шейдерным программам. После завершения шейдера в ряде случаев требуется обнулить используемые им виды, в противном случае ресурс может стать недоступен для остальных шейдерных программ, использующих другой вид данного ресурса.

Также важно иметь в виду, что в момент выполнения кода шейдеров видеодрайвер перестает отвечать на системные запросы, что для пользователя выглядит как полное зависание системы. Поэтому особое значение имеет длительность выполнения шейдерных программ визуализации и обработки воксельных данных. При интенсивной обработке больших объемов данных длительность обработки может превысить таймаут в 2 секунды, в течение которого видеодрайвер должен ответить системе. Если выполнение шейдерной программы не укладывается в данный интервал времени, служба Timeout Detection and Recovery (TDR), работающая в системах Windows Vista/7/Server 2008/Server 2008 R2, сбрасывает выполняющуюся шейдерную программу, тем самым предотвращая зависание системы [11]. Это приводит к тому, что данные для таких шейдеров должны обрабатываться пакетами, время обработки которых укладывается в отведенный таймаут. Для возможности комфортно выполнять фоновую работу в момент интенсивных вычислений на графическом процессоре рекомендуется не отключать службу TDR и использовать функцию Flush для постановки команд графического процессора в очередь.

Для удобной работы с шейдерами Direct3D предлагает систему эффектов [1], которая на сегодня поставляется с открытым исходным кодом вместе с примерами DirectX SDK. Здесь следует сделать отдельное замечание по поводу использования DirectX на .Net Framework. Для этого существует несколько сценариев. Среди готовых решений наиболее полным и производительным на сегодняшний день является SlimDX. В стадии активной разработки также находится SharpDX, который имеет преимущество перед SlimDX в скорости вызовов функций DirectX в силу особенностей реализации. Однако пока SharpDX не предоставляет всех возможностей по работе с DirectX, в частности, он не имеет реализации системы эффектов. Тем не менее, SharpDX претендует на то, чтобы стать более эффективным средством для использования DirectX на .Net Framework в ближайшем будущем [6].

Объемная решетка

На практике настольные компьютеры способны обрабатывать трехмерные текстуры ограниченных размеров D [9]. Типовыми значениями, как правило, являются 256³, 512³ и 1024³. Для обработки воксельных моделей большей размерности предлагается провести разбиение исходной модели на блоки или объемы меньшей размерности. Для удобства будем использовать блоки одинаковых воксельных размеров. Блоки воксельной модели при разбиении образуют множество, которое будем называть объемной решеткой:

φ = {(g, k, s, φ)},

где воксель блока объемной решетки найдется как

φ[g, k, s] = f[g•K + k, s].

Символом «•» в формуле обозначена модуляция векторов. Модуляцией двух и более векторов будем называть вектор, элементы которого равны произведению соответствующих элементов данных векторов, в частности

g•K = {g[i]K[i]}.

Здесь введены:

g = {g[i]} – вектор целочисленных координат блока в объемной решетке, элементы которого принимают значения

g[i] = 0, 1, …, (G[i] - 1);

k = {k[i]} – вектор целочисленных координат точки в локальной системе блока, элементы которого принимают значения

k[i] = 0, 1, …, (K[i] - 1);

K = {K[i]} – вектор размеров блока вдоль осей в соответствующих единичных отрезках;

G = {G[i]} – вектор количества блоков, укладывающихся вдоль соответствующих осей в пределах области определения, элементы которого находятся как

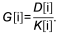
Индекс блока в кортеже принимает значения

c = 0, 1, …, (C - 1),

где общее количество блоков

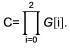
Индекс блока можно вычислить по его координатам в объемной решетке:

c = g[0] + G[0]g[1] + G[0]G[1]g[2].

Предлагаемый вид модели позволяет сократить объем передаваемых данных, тем самым увеличив скорость работы, за счет обработки только тех блоков объемной решетки, которые необходимы в текущем контексте: блоки могут быть невидимы или не затронуты проводимыми построениями. Тем самым может быть осуществлена эффективная обработка больших объемов данных. На рисунке 2 для примера из всей модели заштрихованы визуализируемые блоки объемной решетки, попадающие в пирамиду видимости, часть блоков, выделенных отдельной штриховкой, обрабатывается в ходе ручных операций пользователя. Для обработки всей воксельной модели нужно обработать каждый ее блок последовательно. В каждый момент времени может идти обработка и визуализация только одного блока.

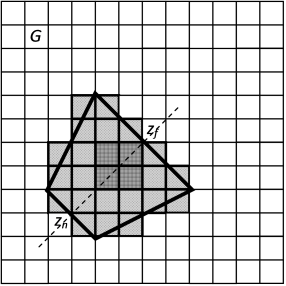
Рисунок 2. Блочная обработка и визуализация модели.

Использование блоков с высокой разрешающей способностью может быть ограничено в силу повышенных требований к вычислительным ресурсам при обработке и визуализации. Например, при разрешающей способности блока равной гигавокселю, т.е. 1024³ вокселей, потребуется 1ГБ памяти без учета остальных необходимых данных. Такой объем данных не может эффективно передаваться между центральным и графическим процессором, а также устройством хранения: базой данных или жестким диском. Для осуществления эффективной обработки и визуализации предлагается разрешающая способность блока, равная 256³.

При решении задач данным методом на практике применяется воксельная модель с размером объемной решетки 12х12х6 при размере блока 256³, что можно записать как 12х12х6@256³. Общий объем данных при этом составляет 13,5 ГБ. Обработка всей модели (включая расчеты и растеризацию) укладывается в максимально допустимый интервал времени в несколько минут. Более крупные размеры модели в целевых задачах в настоящее время не используются.

Растеризация

На практике процесс визуализации неотделим от задач обработки. Опишем процесс получения приведенного на рисунке 1 растрового изображения рассмотренной модели тела, представляющего собой разность куба и шара. Поскольку в целевых задачах метода требуется интерактивная обработка, а фотореалистичным видом изображения можно пренебречь, в основу метода положена растеризация на графическом процессоре.

Чтобы запустить программируемый шейдерный конвейер графического процессора, нам потребуется ввести триангуляционную модель единичного куба, представляющего собой границы блока воксельной модели. Триангуляционная модель в общем случае описывается как кортеж двух множеств [1]

β = {Ψ, E}.

где Ψ = {p[θ]} – множество вершин триангуляции;

θ = 0, 1, …, (Θ - 1) – индекс вершины триангуляции;

Θ – число вершин триангуляции;

p[θ] = {p[θ, j]} – вершина триангуляции;

p[θ, j] ϵ (-∞; +∞) – однородные (гомогенные) координаты;

j = 0, 1, 2, 3 – индекс однородной координаты;

E = {ε[b]} – множество упорядоченных троек индексов вершин триангуляции, образующих треугольник;

b = 0, 1, …, (B - 1) – индекс треугольника;

B – число треугольников;

ε[b] = {ε[b, i]} – грань внешней видимой поверхности моделируемого тела, представляющая собой треугольник, направление обхода вершин которого определяет направление нормали к его поверхности и позволяет обозначить переднюю (лицевую) и заднюю (обратную) стороны грани;

ε[b, i] = 0, 1, …, (Θ - 1) – индекс вершины триангуляции в составе треугольника.

На рисунке 3 приведена триангуляционная модель единичного куба. В таблице 1 перечислены элементы множеств вершин и индексов.

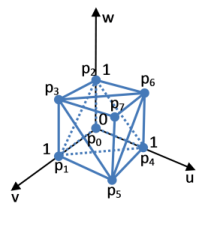
Рисунок 3. Триангуляционная модель единичного куба.

Границы блоков будем рассматривать в единичном кубе объемной решетки. Множество их вершин будем называть узлами объемной решетки (см. рис. 4):

N = {μ[c, θ]},

где μ[c, θ] = {μ[c, θ, i]} – вершина триангуляционного куба границ блока в системе координат объемной решетки.

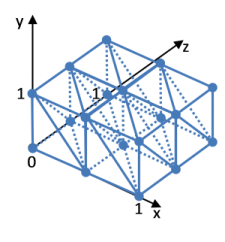
Рисунок 4. Пример объемной решетки 2х2х1.

Введя преобразование переноса как матрицу

где m = {m[i]}, и преобразование масштабирования как матрицу

где s = {s[i]}, найдем узлы объемной решетки как

μ[c, θ] = p[θ]S(x₀)M(c•x₀).

Воксельная модель может иметь произвольное положение, размеры и ориентацию в пространстве. Для их описания введем мировое преобразование узлов объемной решетки, которое задается в виде произведения матриц преобразований переноса, вращения и масштабирования, причем последовательность умножения матриц определяет порядок применения преобразований [1].

Преобразование вращения будем задавать в виде матрицы

R(α) = R(α[0])R(α[1])R(α[2]),

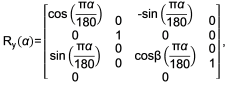
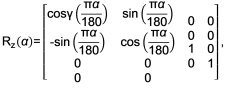
где α = {α[i]} – вектор-строка углов поворота вокруг соответствующих осей в градусах (для расчета тригонометрических функций углы должны быть конвертированы в радианы).

Запишем мировое преобразование как

ω = M(m₀)S(s)R(α)M(m),

где m₀ – вектор-строка переноса центра единичного куба в начало координат; m₀[i] = -0,5.

Узлы объемной решетки в мировой системе координат запишутся в виде:

μ[c, θ]ω = p[θ]S(x₀)M(c•x₀)ω.

Множество преобразований вершин триангуляционных единичных кубов границ блоков в узлы объемной решетки в глобальной системе координат обозначим как

Ω = {W[c]},

W[c] = S(x₀)M(c•x₀)ω.

Чтобы сопоставить с вокселями необходимые при обработке и растеризации параметры, например, материал или текстуру в формате RGBA, плотность вещества и т.п., введем множество так называемых передаточных функций, ставящих в соответствие вокселям векторы параметров [4, 7]:

T = {t[y, v, h]},

где y = 0, 1, …, (Y - 1) – индекс передаточной функции;

Y – число передаточных функций;

t[y, v, h] = {t[y, v, h, λ]} – вектор параметров;

λ = 0, 1, …, (Λ - 1) – индекс параметра;

Λ – количество параметров;

h = 0, 1, …, (H - 1) – аргумент, позволяющий дополнительно варьировать параметры вокселя, например, в зависимости от его глубины H; для однозначного соответствия между вокселем и вектором параметров h = 0.

Передаточные функции для работы на графическом процессоре удобно представить в виде массива двумерных текстур, размер текселя которых равен байтовому размеру элемента вектора параметров.

Таким образом, для растеризации воксельной модели нам понадобятся границы блоков, имеющих векторное описание в виде триангуляционных кубов β, трехмерные текстуры G одинакового размера, сопоставленные каждая со своим блоком, множество передаточных функций T для сопоставления с вокселями необходимых параметров, и преобразований Ω, определяющих положение границ блока в прямоугольной объемной решетке, а также ее положение, ориентацию и размер в глобальных координатах:

Φ = {G, β, T, Ω}.

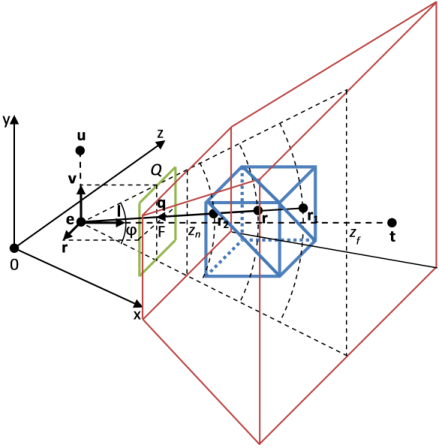
Рисунок 5. Схема растеризации блока.

Результат растеризации удобно рассматривать как кадр, получаемый с виртуальной камеры [1]. Для ее описания зададим видовое преобразование, которое позволяет перейти из глобальной системы координат в локальную систему координат виртуальной камеры (см. рис. 5), в виде матрицы:

где в глобальной системе координат заданы:

e = {e[i]} – положение виртуальной камеры;

a = {a[i]} – точка, на которую направлена камера;

u = {u[i]} – вектор крена камеры;

ρ = {ρ[i]} – орт оси абсцисс локальной системы координат камеры;

v = {v[i]} – орт оси ординат локальной системы координат камеры;

l = {l[i]} – орт оси аппликат локальной системы координат камеры.

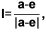
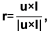
v = l × r.

Символом «×» обозначено векторное произведение.

Процесс получения растрового кадра векторной модели для виртуальной камеры описывается проекционным преобразованием [1]. Оно позволяет спроецировать точки векторного описания модели в системе координат виртуальной камеры на квадрат Q с размером стороны 2 и центром в начале координат в плоскости проекции, параллельной плоскости rev, отстоящей от нее на расстоянии F (см. рис. 5). Тексели квадрата Q q = {q[i]} являются пикселями результирующего растрового изображения размером Q_W×Q_H пикселей. Проецирование выполняется таким образом, что q[0] ϵ [-1; 1], q[1] ϵ [-1; 1], q[2] ϵ [ 0; 1].

Проекционное преобразование будем задавать в виде матрицы перспективной проекции:

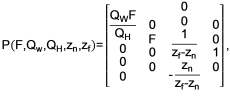
где расстояние от положения камеры до плоскости проекции найдется как

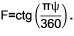
ψ – угол обзора виртуальной камеры в вертикальном направлении в градусах (для расчета тригонометрических функций угол должен быть конвертирован в радианы);

z_n – расстояние от положения камеры до ближней плоскости отсечения;

z_f – расстояние от положения камеры до дальней плоскости отсечения.

Данный вид матрицы в отличие от классического вида задания обеспечивает линейное изменение значений буфера глубины для соответствующего изменения расстояния между проецируемой точкой и ближней плоскостью отсечения, что позволяет устранить нежелательные артефакты при визуализации [3].

Наряду с перспективной проекцией существует также возможность использовать ортографическую проекцию [1].

Введем множество матриц полных преобразований координат вершин единичных триангуляционных кубов границ блоков в координаты спроецированного текселя:

Σ = {σ[c]},

σ[c] = W[c]V(e, a, u)P(F, Q_W, Q_H, z_n, z_f).

Таким образом,

q[c, θ] = p[θ]σ[c].

Напомним, что для получения прямоугольных координат из однородных координат, требуется разделить три первые однородные координаты на их четвертую координату [1].

Особенность воксельной растеризации заключается в том, что цвет и глубина в промежуточных текселях, которые покрываются проецируемым кубом, определяются в результате проецирования текселей (вокселей) трехмерной текстуры блока соответствующим лучом (см. рис. 5). Начало луча r₁ определяется путем линейной интерполяции координат точек поверхности триангуляционного куба растеризатором Direct3D между соответствующими координатами его вершин p[θ] в локальной системе координат куба для опорных точек проекции q[c, θ]. Эта работа выполняется программируемым шейдерным конвейером автоматически для переменной с соответствующей семантикой, например, COLOR [7]. Направление луча r₂ определяется по положению виртуальной камеры в локальной системе координат куба, которое можно найти как

e _b = eW^-1[c],

тогда

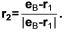
Таким образом, уравнение луча примет вид

r = r₁ + δr₂,

где r = {r[i]}.

Воксели отбираются вдоль луча с шагом

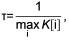
δ’ = δ + τ,

где δ – смещение вдоль луча;

δ’ – смещение вдоль луча на следующем шаге.

Итерации продолжаются до тех пор, пока 0 ≤ r[i] ≤ 1.

Для очередного вокселя через передаточную функцию определяется вектор его параметров t[y, v[r, s], 0]. Далее для цветовых компонентов (каналы RGBA) выполняется альфа-смешивание [4]:

A = A₁ + A₂(1 - A₁),

если A = 0, тогда C = 0, в противном случае

C = C₁A₁ + C₂A(1 - A₁).

где C₁ – компонента цвета накладываемого вокселя;

A₁ – альфа-канал накладываемого вокселя;

C₂ – компонента цвета фонового вокселя;

A₂ – альфа-канал фонового вокселя;

C – компонента цвета результирующего вокселя;

A – альфа-канал результирующего вокселя.

Для последнего вокселя на проецирующем луче, у которого альфа-канал отличен от нуля, координата q[2], которая определяется из соотношения

q = rW[c],

используется для проведения теста глубины [1]. Для возврата глубины из пиксельного шейдера в HLSL используется семантика DEPTH. Тест глубины заключается в сравнении получаемого значения глубины текселя с соответствующим значением глубины, хранящимся в буфере глубины:

z = {z[q[0], q[1]]}.

Тест глубины пройден, если

q[2] < z[q[0], q[1]].

т.е. проецируемое значение не перекрывается ранее спроецированным значением. В этом случае цвет текселя пишется в задний буфер кадра или смешивается с хранящимся там соответствующим значением, а глубина текселя заменяет хранящееся в буфере глубины соответствующее значение:

z[q[0], q[1]] = q[2].

В противном случае вывод текселя в кадр виртуальной камеры не происходит.

На рисунке 6 представлен пример растеризации буфера глубины для тестовой модели.

Рисунок 6. Растеризация буфера глубины тестовой модели.

Наряду с вычислением глубины во время растеризации существует возможность сбора информации, необходимой для ручной обработки воксельной модели пользователем. На рисунках 7-9 представлен пример растеризации буферов для считывания данных, выделяемых мышью, для тестовой модели.

Рисунок 7. Растеризация буфера объемной решетки тестовой модели.

Рисунок 8. Растеризация буфера положений вокселей тестовой модели.

Рисунок 9. Растеризация буфера вокселей тестовой модели.

Также для последнего вокселя на проецирующем луче, у которого альфа-канал отличен от нуля, выполняется затенение с использованием отражательной модели Фонга и одного направленного источника света, что является достаточным для решения большинства целевых задач [1, 4]:

C = C_a + C_dγ + C_s(Rr₂)^SP,

γ = nL,

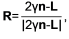
где C – результирующая цветовая компонента;

C_a – составляющая общего цвета для вокселя;

C_d – составляющая рассеивающего цвета для вокселя;

C_s – составляющая зеркального цвета для вокселя;

SP – степень блеска вокселя;

γ – интенсивность падающего света;

n – нормаль к воксельной поверхности в данной точке;

L – вектор направления света;

R – направление отраженного луча света в данной точке.

Опишем способ вычисления нормалей к воксельным поверхностям. Скалярное поле воксельной модели будем рассматривать в текущем состоянии s, т.е. при рассмотрении не будем принимать во внимание его зависимость от времени. Градиент скалярного поля f(x) всегда перпендикулярен поверхностям уровня – множеству точек пространства, в которых скалярное поле принимает одно и то же значение. Поэтому нормаль к воксельной поверхности в данной точке n(x) можно вычислить как градиент скалярного поля. Градиент представляет собой вектор частных производных скалярного поля по направлениям осей системы координат. Частную производную ∂f(x)/∂x[i] рассматриваемого скалярного поля по направлению i-й оси системы координат можно найти как свертку дискретной функции f[k] с ядром фильтра специального вида [12]:

ϕ[i] = {ϕ[i, k_ϕ], k_ϕ},

где k_ϕ = {k_ϕ[i]}, k_ϕ[i]=-D_ϕ[i],-D_ϕ[i] + 1, …, 0, …, D_ϕ[i] - 1, D_ϕ[i] – индексы коэффициентов фильтра;

D _ϕ = {D_ϕ[i]} – радиусы фильтра вдоль соответствующих осей;

ϕ[i, k_ϕ] – коэффициенты фильтра.

Для обозначения свертки будем использовать символ «*».

Запишем

n(x) = {n[k, i]},

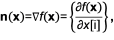
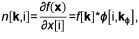
если D_ϕ[i] ≤ k[i] ≤ K[i] - D_ϕ[i], то

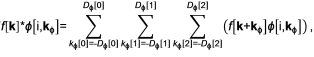
иначе f[k]*ϕ[i, k_ϕ] = 0.

Для отображения гладкой воксельной поверхности нормали необходимо сгладить путем усреднения в окрестности с радиусами вдоль соответствующих осей D_A = {D_A[i]}. Пусть k_A = {k_A[i]}, k_A[i] = -D_A[i],-D_A[i] + 1, …, 0, …, D_A[i] - 1, D_A[i] – индексы элементов окрестности, тогда усредненная или сглаженная нормаль найдется как

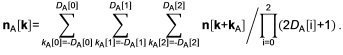
Расчет нормалей и сглаживание эффективнее выполнять при помощи отдельного вычислительного шейдера сразу после изменения воксельных данных. Этот процесс является важной частью обработки модели, необходимой не только для расчета затенения, но и для большинства других операций.

Описанная последовательность операций осуществляется за один проход для одного блока воксельной модели. Чтобы получить растровое изображение всей воксельной модели или отдельной ее части с виртуальной камеры, процедуру необходимо повторить для каждого блока в выборке. Пример растеризации воксельной модели тела, представляющего собой разность куба и шара, рассмотренной ранее, приведен на рисунке 1.

Скорость работы метода зависит от количества и размеров выводимых блоков, пиксельной площади проекции, ориентации камеры относительно объемной решетки (при диагональном ходе проекционных лучей через блоки количество выборок вокселей увеличивается). В таблице 2 приведена средняя тактовая частота обновления экрана для различных стендовых конфигураций при номинальном отображении тестовой модели (2х2х1@256³). Результаты растеризации тестовой модели приведены на рисунке 10.

Рисунок 10. Результат растеризации тестовой модели.

Отдельное замечание следует сделать по поводу однозначного сопоставления вектора параметров вокселям и точечной выборки вокселей из блока. В частности, при этом не используется линейная интерполяция как в других методах [4, 7]. Причиной является то, что воксели рассматриваются как неупорядоченные коды. Интерполяция между кодами приведет к тому, что в точках пространства появятся значения, которые туда не записывались. Например, при рассмотрении воксельной модели месторождения золота с кодами вокселей для воздуха – 0, для руды – 0.5, для породы – 1, при интерполяции значений между вокселями рельефа и воздуха на поверхности земли будет получен слой золота, что будет являться ошибкой.

Заключение

Данный метод разработан для горнодобывающей отрасли и позволяет успешно решать ряд производственных задач горнодобывающих предприятий. Его главные отличительные черты и преимущества перед существующими методами [1, 4, 7] состоят в том, что он максимально прост, является однопроходным, не требует буферных данных о пересечении луча и ограничивающего воксельную модель объема, использует эффективную сегментацию пространства.

Важным преимуществом метода является полноценная реализация штатного теста глубины, что позволяет отображать блоки одной или нескольких воксельных моделей на результирующем растровом изображении с корректным перекрытием, а также совмещать воксельную растеризацию с растеризацией моделей других типов, например, триангуляционных, и осуществлять растеризацию объектов в произвольном порядке.

Достоинством метода является запись буферной информации, служащей для получения данных, выделяемых мышью при ручном редактировании воксельной модели пользователем.

К недостаткам метода следует отнести нецелостную обработку блоков. В результате нормали рассчитываются для границ блоков, при этом целостность карты нормалей монолитного тела не соблюдается. Например, на рисунке 10 четко видны границы между блоками в виде канавок, являющихся визуальным артефактом при расчете затенения. Однако данный недостаток не является существенным для целевых задач метода, и при необходимости могут быть разработаны меры по его устранению.

Воксельные технологии являются перспективным направлением развития трехмерной компьютерной графики. Современный уровень развития аппаратного и программного обеспечения позволяет эффективно применять их для решения различных практических задач. Главным значением рассмотренного метода является то, что он выступает базовой отраслевой платформой для построения комплексных решений и основой для проведения исследований и разработок модификаций.

Список литературы

1. Akenine-Moller, T. Real-Time Rendering. Third Edition / T. Akenine-Moller, E. Haines, N. Hoffman. – Wellesley: A. K. Peters, Ltd., 2008. – 1027 p.
2. Crassin, C. GigaVoxels: Ray-Guided Streaming for Efficient and Detailed Voxel Rendering / C. Crassin, F. Neyret, S. Lefebvre, E. Eisemann // ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games (I3D), feb 2009.
3. Dunlop R. Linearized Depth using Vertex Shaders // Technical Articles / MVPS.org: The X Zone. 2005. URL: http://www.mvps.org/directx/articles/linear_z/linearz.htm (дата обращения: 26.09.2011).
4. Fernando R. GPU Gems: Programming Techniques, Tips and Tricks for Real-Time Graphics / R. Fernando. – Boston: Addison-Wesley Professional, 2004. – 816 p.
5. Green S. DirectCompute Programming Guide // NVIDIA GPU Computing Documentation / NVIDIA Developer Zone. 2010. Систем. требования: PDF Reader. URL: http://developer.download.nvidia.com/compute/DevZone/docs/html/DirectCompute/doc/DirectCompute_Programming_Guide.pdf (дата обращения: 26.09.2011).
6. Mutel A. Benchmarking C#/.Net Direct3D 11 APIs vs native C++ // Code 4k: A blog about coding 4k to 64k intros and demos. 2011. URL: http://code4k.blogspot.com/2011/03/benchmarking-cnet-direct3d-11-apis-vs.html (дата обращения: 26.09.2011).
7. Nguyen H., GPU Gems 3 / H. Nguyen. – Boston: Addison-Wesley Professional, 2007. – 1008 p.
8. numthreads // Reference for HLSL / MSDN Library: Microsoft Software Developer Network Library. 2011. URL: http://msdn.microsoft.com/en-us/library/ff471442(VS.85).aspx (дата обращения: 26.09.2011).
9. Qu, H. Boolean operations of triangulated solids and their applications in the 3D geological modeling // ISPRS: International Society for Photogrammetry and Remote Sensing. 2011. Систем. требования: PDF Reader. URL: http://www.isprs.org/proceedings/xxxvi/2-w25/source/boolean operations of triangulated solids and their applications in the 3d geological modelling.pdf (дата обращения: 26.09.2011).
10. Resource Limits (Direct3D 11) // Programming Guide for Direct3D 11 / MSDN Library: Microsoft Software Developer Network Library. 2011. URL: http://msdn.microsoft.com/en-us/library/ff819065(v=VS.85).aspx (дата обращения: 26.09.2011).
11. Timeout Detection and Recovery of GPUs through WDDM // Windows Dev Center – Hardware. 2009. URL: http://msdn.microsoft.com/en-us/windows/hardware/gg487368 (дата обращения: 26.09.2011).
12. Грузман, И. С. Цифровая обработка изображений в информационных системах / И. С. Грузман. Уч. пособие. – Новосибирск: НГТУ, 2002. – 168 с.
13. Мальцев А. И. Алгебраические системы / А. И. Мальцев. – М.: Наука, 1970. – 302 с.

Сообщений 0    Оценка 50 [+0/-1]         Оценить